Bonjour tout le monde,
J'ai quelques soucis pour un de mes DM de maths de term S.
Voici l'énoncé : " Soit (un) une suite définie par Uo appartient à R et pour tout n de N : Un+1 = f(un) où f est une fontcion définie sur une partie D de R et à valeurs dans R. Un intervalle I de R ( I c D ) est dit stable par f lorsque f(I) c I. Soit I un tel intervalle
1) Montrer que si Uo appartient à I, alors pour tout n de N, Un est bien défini et appartient à I
2) Montrer que si f est croissante sur I alors la suite (un) est monotone. Par quoi est alors déterminé son sens de variation ?
3) Montrer que, si pour tout x de I, f(x) supérieur ou egal à x, alors la suite (un) est croissante.
4) Montrer que, si pour tout x de I, f(x) inférieur ou égal à x, alors la suite (un) est décroissante.
Si vous pouviez me donner quelques pistes de réfléxions, cela m'arrangerait bien. Merci, bonne journée.
Intervalle
9 messages
- Page 1 sur 1
Bonjour,
Du grand n'importe quoi. Fais un peu attention aux notations.
D'abord un c'est . Ensuite tu utilises tantôt les minuscules tantôt les majuscules pour désigner la suite; la casse est importante:
. Ensuite tu utilises tantôt les minuscules tantôt les majuscules pour désigner la suite; la casse est importante: ) et
et ) ne désignent pas la même suite. Enfin +1 doit être en indice. Comment faire la différence entre
ne désignent pas la même suite. Enfin +1 doit être en indice. Comment faire la différence entre 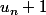 et
et  avec ta notation ? Un peu de bon sens voyons. Une suite est une fonction sur
avec ta notation ? Un peu de bon sens voyons. Une suite est une fonction sur  donc utilise la notation fonctionnelle; cela donne u(n+1)=f(u(n)) pour
donc utilise la notation fonctionnelle; cela donne u(n+1)=f(u(n)) pour ) .
.
Pour des suites de la forme) tu devras souvent faire des démonstrations par récurrence. Evidemment pour démontrer l'hérédité tu auras besoin d'utiliser les propriétés de f. Ca peut être une bonne idée pour t'aider d'avoir sous les yeux un tableau de variation de f ainsi que sa courbe représentative.
tu devras souvent faire des démonstrations par récurrence. Evidemment pour démontrer l'hérédité tu auras besoin d'utiliser les propriétés de f. Ca peut être une bonne idée pour t'aider d'avoir sous les yeux un tableau de variation de f ainsi que sa courbe représentative.
Ihalla newton a écrit:pour tout n de N : Un+1 = f(un)
Du grand n'importe quoi. Fais un peu attention aux notations.
D'abord un c'est
Si vous pouviez me donner quelques pistes de réfléxions, cela m'arrangerait bien. Merci, bonne journée.
Pour des suites de la forme
SaintAmand a écrit:Bonjour,
Du grand n'importe quoi. Fais un peu attention aux notations.
D'abord un c'est. Ensuite tu utilises tantôt les minuscules tantôt les majuscules pour désigner la suite; la casse est importante:
et
ne désignent pas la même suite. Enfin +1 doit être en indice. Comment faire la différence entre
et
avec ta notation ? Un peu de bon sens voyons. Une suite est une fonction sur
donc utilise la notation fonctionnelle; cela donne u(n+1)=f(u(n)) pour
.
Pour des suites de la formetu devras souvent faire des démonstrations par récurrence. Evidemment pour démontrer l'hérédité tu auras besoin d'utiliser les propriétés de f. Ca peut être une bonne idée pour t'aider d'avoir sous les yeux un tableau de variation de f ainsi que sa courbe représentative.
Cependant j'ai peur de dire une bêtise, mais nous ne connaissons pas la valeur de la fonction f, nous connaissons juste que u(n+1)=f(u(n)) Merci de ton commentaire en tout cas.
Ihalla newton a écrit:Cependant j'ai peur de dire une bêtise, mais nous ne connaissons pas la valeur de la fonction f, nous connaissons juste que u(n+1)=f(u(n)) Merci de ton commentaire en tout cas.
Tu as quand même des informations sur f. Par exemple pour démontrer que la suite est monotone si f est croissante, dessine le graphe d'une fonction croissante, choisis un u(0) quelconque, et représente sur le graphe les premiers termes. Eventuellement multiplie les exemples. Tu devrais rapidement comprendre ce qui se passe.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
