Repère et vecteur

[vince_57]

Bonjour j'ai un problème avec l'exercice suivant:

On donne les points A(5;1),B(-2;1) et C(0;4)

1)Calculez les coordonnées (x;y) du point M défini par:

+ + =

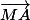
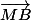
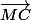
2)Représenter le triangle ABC et le point M

MA=MB=MC

J'aimerais donc savoir s'il faut que j'utilise la propriété du cercle circonscrit en prouvant que le triangle ABC est rectangle en C.Et vu que le centre du cercle circonscrit est le milieu de l'hypoténuse alors je n'aurais plus qu'à calculé les coordonnées de M sachant qu'il est le milieu de BA

Merci d'avance

[fafaf00]

Oui c'est exactement ca ;o)

[vince_57]

Oui c'est exactement ca ;o)

mais je ne trouve pas BA²=BC²+CA²

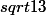
J'ai trouvé : ² = ² + ²

ce qui n'est pas le cas :help:

[Carpate]

Bonjour j'ai un problème avec l'exercice suivant:

On donne les points A(5;1),B(-2;1) et C(0;4)

1)Calculez les coordonnées (x;y) du point M défini par:

+ + =

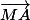
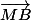
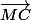
2)Représenter le triangle ABC et le point M

MA=MB=MC

J'aimerais donc savoir s'il faut que j'utilise la propriété du cercle circonscrit en prouvant que le triangle ABC est rectangle en C.Et vu que le centre du cercle circonscrit est le milieu de l'hypoténuse alors je n'aurais plus qu'à calculé les coordonnées de M sachant qu'il est le milieu de BA

Merci d'avance

Bonjour,
Qu'est-ce qui te permet d'affirmer que ABC est rectangle en C ?
Calcule les composantes des vecteurs et écrit que
la somme de ces 3 vecteurs est le vecteur nul

Edit : je n'avais pas vu qu'il y avait déjà des réponses quand j'ai répondu ...

[Dlzlogic]

mais je ne trouve pas BA²=BC²+CA²

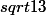
J'ai trouvé : ² = ² + ²

ce qui n'est pas le cas :help:

Bonjour,
Qui a dit que le triangle ABC était rectangle en C ?

[vince_57]

Bonjour,
Qui a dit que le triangle ABC était rectangle en C ?

Et bien si BA est l'hypoténuse le triangle devrait être rectangle en C non ? :mur:

[vince_57]

Bonjour,
Qu'est-ce qui te permet d'affirmer que ABC est rectangle en C ?
Calcule les composantes des vecteurs et écrit que
la somme de ces 3 vecteurs est le vecteur nul

Edit : je n'avais pas vu qu'il y avait déjà des réponses quand j'ai répondu ...

Mais comment les calculés :hum:

[vince_57]

M est le milieu du segment [BA] car M est le centre de gravité du triangle ABC, donc:

xM=(xA+xB)=5+(-2)/2=3/2=1.5
yM=(yA+yB)=1+1/2=2/2=1

Les coordonnées du point M sont (1.5 ; 1)

:hein:

[Carpate]

Mais comment les calculés :hum:

Mais comment les calculer

De manière générale :

[Dlzlogic]

M est le milieu du segment [BA] car M est le centre de gravité du triangle ABC, donc:

xM=(xA+xB)=5+(-2)/2=3/2=1.5
yM=(yA+yB)=1+1/2=2/2=1

Les coordonnées du point M sont (1.5 ; 1)

:hein:

Qui a dit que M est le milieu de AB ?
Bien sûr vous êtes parti sur une fausse piste dès le départ.
Reprenez le problème à la base et ne prenez comme certitude que ce que vous pouvez démontrer.