Bonjour j'ai un devoir de math a rendre, mais je bute dès le début, je ne sait pas comment commencer.
J'aimerais que l'on me débloque. Merci d'avance.
On se propose détudier les fonctions f dérivables sur R qui vérifient :
F(0)=1 et f=af où a est un réel donné (*)
A. Partie informatique
On souhaite construire avec la méthode dEuler des courbes approchées de la fonction f.
Pour cela, on obtient les coordonnées de 200 points en créant :
- une liste de 200 abscisses (xn) telles que x100 et, pour tout n appartenant à N ,
xn+1=xn+0,05
- Une liste de 200 ordonnées (yn) telles pour tout n appartenant à N , soit calculé par une
approximation affine de f(xn)
1. a. Exprimer y101 lapproximation affine de f(0,05) en fonction de y100 et a.
b. Plus généralement, donner la relation entre yn+1 et ,pour yn puis la formule
associée à y101 que lon va ensuite étirer.
2. a. Exprimer y99 lapproximation affine de f(-0,05) en fonction de y100 et a.
b. Plus généralement, donner la relation entre yn-1 et yn ,pour n inférieur ou égale à 100 puis la formule
associée à que lon va ensuite étirer.
3. Construction de la feuille de calcul
a. Attribuer une cellule à la valeur de la constante a de façon à pouvoir la
modifier. On prendra pour le début a=1.
b. Construire les listes (xn) et (yn) dans 2 colonnes. Ne pas oublier de fixer ladresse de la cellule contenant a avec un $.
c. Afficher la courbe correspondant au nuage des 200 points en réglant correctement la fenêtre.
4. Observation des résultats obtenues pour différentes valeurs de a.
a. Pour a=1 , quelle courbe reconnaissez vous ?
b. Donner les variations et les limites observées en fonctions des valeurs de a.
(Ne pas oublier dessayer avec des valeurs négatives de a)
B Partie mathématique
1. Soit h(x)= expodentielle (ax)
a. Déterminer la fonction u telle que h= exp rond u
b. Après avoir justifié que h est dérivable sur R, calculer sa dérivée .
2. Soit g(x)=f(x)/exp(ax) où f est une fonction qui vérifie (*)
a. Justifier que g est une fonction dérivable sur R
b. Démontrer que g est une fonction constante sur R.
c. Conclure : Combien de fonctions vérifient la condition (*) ? quelles sont leurs
expressions ?
3. Démontrer les résultats observés à la question 4.b. de la partie A
Pour la question A1a, faut il utiliser la formule de l'approximation affine: f(a+h)=f(a)+f'(a)(h-a)?
Cordialement, Léo
Devoir terminale S, Euler
8 messages
- Page 1 sur 1
Indication
@Collin
Bonjour
La méthode d'Euler consiste à "approximer" les valeurs d'une fonction dérivable à partir des ses différentes tangentes.
Pour trouver cette relation
1) il faut calculer l'équation de la tangente en un point c'est à dire une équation d'une droite de type
c'est à dire une équation d'une droite de type ) ( en fonction de
( en fonction de  ,
, 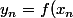) et
et ) )
)
2) calculer sur cette tangente l'ordonnée du point en c'est à dire le point d'ordonnée
c'est à dire le point d'ordonnée  )
)
3) puis écrire que si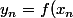) et si
et si ) , alors on a la relation
, alors on a la relation 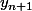 ~~
~~)
Bonjour
La méthode d'Euler consiste à "approximer" les valeurs d'une fonction dérivable à partir des ses différentes tangentes.
Pour trouver cette relation
1) il faut calculer l'équation de la tangente en un point
2) calculer sur cette tangente l'ordonnée du point en
3) puis écrire que si
BonsoirCollin a écrit:Pour la question B2: Pour justifier que g est dérivable comment fait on?
Pour g une fonction constante, on doit montrer que la dérivé de g égale 0?
Que me demande t-on pour la question C?
Merci
a) Il faut expliquer pourquoi la fonction définie par g(x)=f(x)/exp(ax) est dérivable sur IR
b) Comme f'=af , on peut démontrer que pour tout x de IR on a g'(x)=0 et donc que g est une fonction constante sur IR
c) comme
ET comme on a : f(x)=k.exp(ax)
la question est : combien y-a-t-il de fonction
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
