Limite qui tend vers e
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 12:13
par avis91 » 06 Jan 2011, 12:13
Bonjour
je dois démontrer une inéquation et je n'arrive pas trop
e^x>1+x (1) en utilisant (1) je dois démontrer que pour tout n>0; (1+(1/n))^n<e
Merci d'avance.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 06 Jan 2011, 12:15
par Sylviel » 06 Jan 2011, 12:15
Quel x choisir a priori ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 12:35
par avis91 » 06 Jan 2011, 12:35
oh pardon à la base c'est une suite Un=(1+(1/n))^n
et je dois démontrer a l'aide de (1)e^x>1+x que pour tout n>0 UnMerci
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 06 Jan 2011, 12:43
par Sylviel » 06 Jan 2011, 12:43
oui j'ai bien compris, je te demande quel x choisir dans 1) pour te rapprocher du résultat ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 12:45
par avis91 » 06 Jan 2011, 12:45
surement x=1
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 06 Jan 2011, 12:52
par Sylviel » 06 Jan 2011, 12:52
Non, x=1 ne te donneras jamais de n... Regarde un peu ce que tu as :
e^x>1+x
et ce que tu veux montrer :
(1+(1/n))^n
quel x peux tu prendre ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 13:03
par avis91 » 06 Jan 2011, 13:03
oui je vois e^n>1+n
((e^n)/n)>((1+n)/n) (car n>0)
((e^n)/n)^n>((1+n)/n)^n à droite j'ai retrouver l'egalité mais à gauche je ne
sais pas comment faire.
merci

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 06 Jan 2011, 13:31
par Olympus » 06 Jan 2011, 13:31
Tu veux montrer que
^n)
.
Première chose, essaie de mettre cette inégalité sous la forme

. D'abord, l'exposant
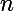
dans l'inégalité à prouver gène, tu feras comment pour t'en débarrasser ?
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 13:52
par avis91 » 06 Jan 2011, 13:52
Je ne sais pas quel X prendre. je suis completement perdu :mur:
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 14:04
par avis91 » 06 Jan 2011, 14:04
ok je trouve x=1/n est-ce que c'est bon?
-
Anonyme
 par Anonyme » 06 Jan 2011, 14:07
par Anonyme » 06 Jan 2011, 14:07
Mais c'est pas fini ..
En prenant
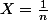
que devient ton inégalité ?
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 14:31
par avis91 » 06 Jan 2011, 14:31
j'ai réussi a démontrer la premiere mais je bloque sur une autre inégalité (-1/(e^n+1))<(n/(n+1)).
Merci de m'aider.
-
Anonyme
 par Anonyme » 06 Jan 2011, 14:38
par Anonyme » 06 Jan 2011, 14:38
c'est bien

?
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 14:42
par avis91 » 06 Jan 2011, 14:42
non c'est e^(n+1)
-
Anonyme
 par Anonyme » 06 Jan 2011, 14:49
par Anonyme » 06 Jan 2011, 14:49

Si c'est ça alors c'est trivial , l'un est négatif alors que l'autre est positif .
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 14:59
par avis91 » 06 Jan 2011, 14:59
Desolé je me suis trompé. La question c'est e^(-1/(n+1))> n/(n+1).
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 15:04
par avis91 » 06 Jan 2011, 15:04
est-ce qu'il faut prendre X=-1/(n+1)?
-
Anonyme
 par Anonyme » 06 Jan 2011, 15:08
par Anonyme » 06 Jan 2011, 15:08
Essaye , ça prend 20s :)
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 15:14
par avis91 » 06 Jan 2011, 15:14
Merci......
-
avis91
- Membre Naturel
- Messages: 15
- Enregistré le: 12 Nov 2010, 19:20
-
 par avis91 » 06 Jan 2011, 15:39
par avis91 » 06 Jan 2011, 15:39
Une dernière question:
Un= (1+(1/n))^n
Montrer que Un+1/Un> ((n+2)/(n+1)) (1-(n/(n+1)²));
[on pourra utiliser que pour tout a>-1 (1+a)^n> 1+na]
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 114 invités
