[DM de 1ère S] Fonctions, vecteurs et trigonométrie

[SteezyRider]

Bonjour,

J'ai un DM de mathématiques et je n'arrive pas à répondre à certaines questions. J'ai réussi l'exercice 2, et je bloque à la 2. c) de l'exercice 1, ainsi qu'à l'exercice 3.



Je pensais à utiliser des vecteurs pour la 2. c), et la trigonométrie pour l'exercice 3, mais je bloque.


Pouvez vous m'aider s'il vous plait ?

Merci d'avance.

[arnaud32]

pour le 3) comment ecris tu l'aire du rectangle en question en fonction de l'angle et du rayon?

[SteezyRider]

cos angle * sin angle = aire

Non ?

[arnaud32]

donc A(x)=Sin(x)*Cos(x) sur [0,pi/2]
si ca a un maximum tu peux le trouver comment?

[Jimm15]

Coucou,

Je ne comprends pas pourquoi tu bloques à la 2. c. Tout dépend en fait de comment tu t’y es pris pour répondre à la question précédente.

[SteezyRider]

donc A(x)=Sin(x)*Cos(x) sur [0,pi/2]
si ca a un maximum tu peux le trouver comment?

Je suis désolé mais après avoir cherché je ne vois vraiment pas quelle propriété trigonométrique je dois utiliser...

Coucou,

Je ne comprends pas pourquoi tu bloques à la 2. c. Tout dépend en fait de comment tu t’y es pris pour répondre à la question précédente.

J'ai oublié de préciser qu'en fait, c'est la deuxième partie de la 2. c) à laquelle je bloque. Pour 2. c) première partie de la question, j'ai trouvé que P et Dm ont 2 points d'intersection distincts pour M > -1. Mais je ne trouve pas l'ensemble des points Im.

[arnaud32]

et si tu derivais ta fonction? et que tu regardais ses variations?

[SteezyRider]

et si tu derivais ta fonction? et que tu regardais ses variations?

Je n'ai pas encore appris à faire cela.

[arnaud32]

et sin(x)cos(x)=1/2Sin(2x) ?

[SteezyRider]

et sin(x)cos(x)=1/2Sin(2x) ?

Oui ça oui.

Mais j'ai du mal à cerner en quoi cela pourrait m'être utile... :hum:

[arnaud32]

tu as une aire qui vaut
et tu veux le maximum.
que vaut sin(2x) au maximum? pour quelle valeur de x?

[SteezyRider]

sin(2x) vaut 1 au maximum, donc, comme on sait que 1 = sin(Pi/2) donc on a sin(2x) = sin(Pi/2) donc x vaut Pi/4, et alors on cos(x) avec x = Pi/4 aussi (donc une valeur de 2 racine carrée de 2 pour les côtés).

C'est ça ?

Par contre, je ne comprends pas d'où tu sors ...

[arnaud32]

tu as A = sin(x)cos(x)=1/2Sin(2x)
puis tu fais sin(2x)=1 ssi 2x=pi/2 [pi] donc x=pi/4 [pi/2]
tu travailles dans [0,pi/2] si j'ai bonne memoire
donc la seule solution est x=pi/4

[SteezyRider]

D'accord, merci beaucoup, j'ai tout compris ! Notre professeur de mathématiques nous avait prévenu que cet exercice était assez compliqué pour notre niveau actuel en trigonométrie.

D'autres idées pour la deuxième partie du 2. c) ? Faut-il utiliser les vecteurs ou bien les trinômes du second degré ? Merci d'avance.

[Jimm15]

Bonsoir,

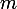
Qu’est-ce que représente pour la droite ? Lorsque varie, quel est le point commun (géométrique) des droites obtenues ? De plus, la fonction carrée est ..... donc que se passe-t-il pour le milieu des deux points d’intersection de et ?

N’hésite pas à utiliser ta calculatrice en traçant simultanément :
– la courbe de ;
– plusieurs droites (par exemple, , , ).

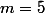
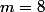
[SteezyRider]

A part que Im représente le milieu de Dm, et que le -2x reste identique, je ne vois pas autre chose qui pourrait m'aider...
J'ai cependant réussi à conjecturer que l'ensemble des points Im est la droite d'équation x = -1 , mais je n'arrive pas à la démontrer...

[Jimm15]

Bonsoir,

Les droites sont parallèles et est paire. Comme est le milieu du segment reliant les deux points d’intersection de et , se déplace sur une droite verticale (les segments étant aussi parallèles). On ne te demande pas, a priori, d’en préciser l’équation, donc cette justification suffit à mon avis.