Devoir au choix
27 messages
- Page 1 sur 2 - 1, 2
Devoir au choix
Salut
C'est mon premier poste ici et je me dis dommage que j'ai pas connu le forum bien avant :ptdr:
Voilà depuis quelques semaines, mon professeur nous a donné un certain devoir qui sera compté comme un + mais j'arrive toujours pas à le résoudre. Je pense que c'est au dessus de mon niveau.
;) n;)24 (a,b) N²
démontrez que n=5a+7b
Pour préciser je suis en premiere :we:
Merciii
C'est mon premier poste ici et je me dis dommage que j'ai pas connu le forum bien avant :ptdr:
Voilà depuis quelques semaines, mon professeur nous a donné un certain devoir qui sera compté comme un + mais j'arrive toujours pas à le résoudre. Je pense que c'est au dessus de mon niveau.
;) n;)24 (a,b) N²
démontrez que n=5a+7b
Pour préciser je suis en premiere :we:
Merciii
Moi je serais plutôt pour une étude en différenciant selon les restes de la division par 5. ie tout n peux s'écrire n = 5*q + r, où r = 0, 1, 2, 3 ou 4. Dans chacun de ces cas tu peux construire ton a et ton b. Bonne recherche !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Salut,
Si tu veut faire une récurrence (ce n'est pas l'outil vraiment adapté à ce problème, mais l'outil adapté... on ne le voit qu'en spécialité de term S...), il faut te poser la question de comment passer de n=5a+7b à n+1=5a'+7b' (ce ne sont évidement pas les mêmes a et b)
Et, pour ce faire, il faut évidement se poser la question "où est donc passé le +1 ?".
Bien sûr, il est "rentré" dans le 5a et le 7b (ce qui a provoqué leur changement de valeurs) donc il faut chercher comment écrire 1 sous la forme 1=5.?+7.? où les ? sont des entiers pas trop grand (mais pas forcément positifs...)
Une fois que tu as trouvé DEUX solutions "pas trop grandes", tu peut attaquer ta récurence (en distinguant deux cas dans l'hérédité...)
Tu peut essayer d'écrire 24 puis 25 puis 26 puis 27 puis 28... sous la forme 5a+7b puis essayer de voir comment on passe de l'écriture de 24 à celle de 25, de celle de 25 à celle de 26, etc
(re)indication : il y a deux cas de figure...
Si tu veut faire une récurrence (ce n'est pas l'outil vraiment adapté à ce problème, mais l'outil adapté... on ne le voit qu'en spécialité de term S...), il faut te poser la question de comment passer de n=5a+7b à n+1=5a'+7b' (ce ne sont évidement pas les mêmes a et b)
Et, pour ce faire, il faut évidement se poser la question "où est donc passé le +1 ?".
Bien sûr, il est "rentré" dans le 5a et le 7b (ce qui a provoqué leur changement de valeurs) donc il faut chercher comment écrire 1 sous la forme 1=5.?+7.? où les ? sont des entiers pas trop grand (mais pas forcément positifs...)
Une fois que tu as trouvé DEUX solutions "pas trop grandes", tu peut attaquer ta récurence (en distinguant deux cas dans l'hérédité...)
Tu peut essayer d'écrire 24 puis 25 puis 26 puis 27 puis 28... sous la forme 5a+7b puis essayer de voir comment on passe de l'écriture de 24 à celle de 25, de celle de 25 à celle de 26, etc
(re)indication : il y a deux cas de figure...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Darxi07 a écrit:J'ai essayé cette méthode mais j'ai pas pu remarquer ce qu'il faut
Voilà les nombres que j'ai utilisé :
N+1=5a+7b+1
N+1=5A+7B+15-14
N+2=5A+7B+2
N+2=5A+7b-5+7
N+3=5A+7B+3
N+3=5A+7B+10-7
La moitié de la solution est dans ta première ligne, mais les autres ne sont pas utiles car, dans une récurrence, il suffit d'expliquer comment on passe de n à n+1.
L'amorce de la récurence (avec
Pour l'hérédité, on considère un
Comme tu l'as écrit, on a alors :
Essaye de trouver une deuxième façon d'écrire n+1 qui marcherais lorsque b est trop petit (donc une écriture qui fasse augmenter le
Une GROSSE indication : trouve comment s'écrit 25 sous la forme 5a+7b puis regarde comment s'écrit 26 sous la forme 5a+7b. Comment est on passé de l'une à l'autre ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Darxi07 a écrit:Oouch j'espere que c'est ce qui est voulu
25 = 5(2+3)+7(2-2)
26= 5(-2+3)+7(5-2)
Oui, mais j'aurais plutôt écrit :
25 = 5.5+7.0=5.a+7.b avec a=5 et b=0
26 = 5.1+7.3=5.a'+7.b' avec a'=1=a-4 et b'=3=0+3
qui permet d'avoir l'idée d'écrire que, quelque soient a et b, on a
(5a+7b) + 1 = 5(a-4)+7(b+3) qui va "faire marcher" la récurrence... mais uniquement si a>=4.
Reste à expliquer pourquoi on est sûr que b>=2 ou bien a>=4 (et donc qu'il y a au moins un des deux trucs qui marche)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Effectivement, de loin, les problèmes se ressembles, mais en fait c'est nettement plus complexe sur N du fait que certaines soustractions sont interdites dans N.Darxi07 a écrit:Ahe c'est là où tu voulais en venir, j'ai déjà fait une fois à peu près la meme chose sauf que pour que ça soit juste il faut que a et b appartiennent à Z et pas N
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si, tu devrait y arriver : tu as tout les éléments dans les diférents posts au dessus :
Faire une récurrence et, dans la récurrence, distinguer deux (ou trois, ça dépend comment on compte...) cas.
Tu as presque toute la preuve dans le post du 05/11/2010 à 23h22...
Faire une récurrence et, dans la récurrence, distinguer deux (ou trois, ça dépend comment on compte...) cas.
Tu as presque toute la preuve dans le post du 05/11/2010 à 23h22...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Si, tu devrait y arriver : tu as tout les éléments dans les diférents posts au dessus :
Faire une récurrence et, dans la récurrence, distinguer deux (ou trois, ça dépend comment on compte...) cas.
Tu as presque toute la preuve dans le post du 05/11/2010 à 23h22...
Dur dur.. j'ai jamais étudié cette leçon pour la verification je pense qu'on a dépassé ce stade après tous les postes qui précèdent.
Je comprends pas au juste comment démontrer n+1 vu que ce n'est meme pas juste pour 'n' si a et b n'appartiennent pas à N
Bon, je te donne "presque tout" :
On veut montrer que tout entier peut s'écrire
peut s'écrire 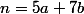 avec
avec  et
et 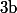 entiers naturels.
entiers naturels.
On procède par récurrence :
Amorce : donc la propriété est vraie pour
donc la propriété est vraie pour 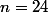 .
.
Hérédité : On considère un fixé et on suppose qu'il sécrit
fixé et on suppose qu'il sécrit 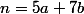 avec
avec  et
et 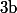 dans
dans 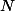 .
.
- Si alors on peut écrire
alors on peut écrire +7(b+3)) où
où  et
et  sont des entiers naturels donc la propriété est bien vérifiée par
sont des entiers naturels donc la propriété est bien vérifiée par  .
.
- Si alors on peut écrire
alors on peut écrire +7(b-2)) où
où  et
et  sont des entiers naturels donc
sont des entiers naturels donc  la propriété est bien vérifiée par
la propriété est bien vérifiée par  .
.
- Si et
et  alors
alors 
On veut montrer que tout entier
On procède par récurrence :
Amorce :
Hérédité : On considère un
- Si
- Si
- Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
sans récurrence cela va assez vite.
les 5a feront tous les nombres se terminant par 0 et 5
pour le reste les 5a feront les paquets de 10
couplés à
0+7=7
0+14=14
0+21=21,
donc on a déjà tous les nombres se terminant par 0,1,4,5,7
ensuite des 5(a-1) feront avec
5+7=12 fera tous les 2
5+14=19 fera tous les 9
5+21=26 fera tous les 6
5+28=33 fera tous les 3
donc on sait fabriquer tous les nombres se terminant par 0,1,2,3,4,5,6,7,8,9
les 5a feront tous les nombres se terminant par 0 et 5
pour le reste les 5a feront les paquets de 10
couplés à
0+7=7
0+14=14
0+21=21,
donc on a déjà tous les nombres se terminant par 0,1,4,5,7
ensuite des 5(a-1) feront avec
5+7=12 fera tous les 2
5+14=19 fera tous les 9
5+21=26 fera tous les 6
5+28=33 fera tous les 3
donc on sait fabriquer tous les nombres se terminant par 0,1,2,3,4,5,6,7,8,9
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Ah donc
Si a;)3 et b;)1 n=5a+7b;)24
ce qui est pas le cas qu'on est en train d étudier ?
Désolé Beagle j'ai pas arrivé à raisonner ce que tu as écrit et je suis aussi obligé à utiliser la recurrence (selon le prof ) :(
-----------------------------------------
Bon voilà ce que j'ai fait
n=5a+7b
n=5(2)+7(2) ce qui est plus grand ou égal 24
n est juste
j'ai remplacé n par n=5(a+7)+7(b-5) (les 7 et -5 proviennent de 35-35=0)
n+1=5(a+3)+7(b-2)
selon n
b est plus grand ou égal 2
donc
7(b-2) prendra au moins la valeur 0 et 0 N
donc n+1 est juste
Si a;)3 et b;)1 n=5a+7b;)24
ce qui est pas le cas qu'on est en train d étudier ?
Désolé Beagle j'ai pas arrivé à raisonner ce que tu as écrit et je suis aussi obligé à utiliser la recurrence (selon le prof ) :(
-----------------------------------------
Bon voilà ce que j'ai fait
n=5a+7b
n=5(2)+7(2) ce qui est plus grand ou égal 24
n est juste
j'ai remplacé n par n=5(a+7)+7(b-5) (les 7 et -5 proviennent de 35-35=0)
n+1=5(a+3)+7(b-2)
selon n
b est plus grand ou égal 2
donc
7(b-2) prendra au moins la valeur 0 et 0 N
donc n+1 est juste
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
