Déduire Coordonnées par Equation

[Howto]

Bonjour à tous, je bloque sur une petite question de mon DM :

Le cercle C coupe l'axe des ordonnées en F et G.
4.a) (fait) Démontrez que les coordonnées y de ces points sont solutions de l'équation :
(y + 1/2 )² = 49/4

Jusque là, pas de soucis, S = 12.25

Mais, 4.b) Déduisez en les coordonnées de F et G.

Comment faire pour celle là ? Quelle méthode ?
Merci d'avance !

[Ericovitchi]

on a pas l’énoncé donc je ne voudrais pas te dire de bêtise mais déjà si tu dis que tes deux points sont solutions de (y + 1/2 )² = 49/4 tu vas trouver les deux y qui satisfont cette équation
(y+1/2)=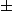 7/2 d'où les y

Et puis après comme ils sont sur l'axe des ordonnées, leur x=0

(par contre S = 12.25 ça je n'ai pas compris ce que tu voulais dire).

[johnjohnjohn]

Bonjour à tous, je bloque sur une petite question de mon DM :

Le cercle C coupe l'axe des ordonnées en F et G.
4.a) (fait) Démontrez que les coordonnées y de ces points sont solutions de l'équation :
(y + 1/2 )² = 49/4

Jusque là, pas de soucis, S = 12.25

Mais, 4.b) Déduisez en les coordonnées de F et G.

Comment faire pour celle là ? Quelle méthode ?
Merci d'avance !

S = 12.25 ? FAUX !

(y + 1/2 )² = 49/4 ssi (y + 1/2 )² - 49/4 =0 ssi (y + 1/2 - 7/2 )(y + 1/2 +7/2 ) = 0 ssi .....