Jai besoin d'aide , cet exercice est un peu difficile

[Jihane89]

soit x et y deux nombres réel.
et que x²+y²=10
et x*x*xy+x²y²+xy*y*y=39
Montrez que
x+y=4 ou x+y=-4

[Sve@r]

C'est niveau collège ça ???

[gigamesh]

salut,
joli comme exercice, mais le mettre dans "collège et primaire" c'est bizarre, non ?

Quelques indices :
*Pars de et multiplie les deux membres par
*Pose ; il faudra résoudre pour trouver ce X
*En connaissant et , tu peux trouver

Bon courage !

[gigamesh]

C'est niveau collège ça ???

hum...

pour un bon élève de troisième, c'est jouable.

Ou bien dans un pays où les collégiens ont un programme de maths un peu costaud...

Bon à mon époque les fonctions y compris bijections injections surjections c'était au CM2, et les structures algébriques (groupes anneaux corps) en cinquième...

[Jihane89]

Oui c'es niveau college ..

[Sve@r]

Oui c'es niveau college ..

Ok. Ben gigamesh t'a donné la méthode...

[Jihane89]

Mais je n'ai toujours rien compris :hein:

[Jihane89]

soit x et y deux nombres réel.
et que x²+y²=10
et x*x*xy+x²y²+xy*y*y=39
Montrez que
x+y=4 ou x+y=-4

[gigamesh]

Bon voila une méthode plus simple :

* Mets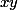 en facteur dans le membre gauche de la deuxième égalité :

se réécrit
* Ensuite tu peux remplacer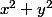 par 10.
Donc l'équation se réécrit xy(...+10)=39

*Ajoute 25 aux deux membres
*Factorise le membre gauche avec une identité remarquable
*soustrait 64 aux deux membres
*Factorise le membre gauche
*Un produit est nul quand un facteur est nul

Tu auras alors trouvé xy

[Jihane89]

xy(x²+xy+y2)=39
xy(10+xy)=39
(xy+5)²=39+25
(xy+5-8)(xy+5+8)=0
(xy-3)(xy+13)=0
xy=3 ou xy=-13
c'est sa ?

[gigamesh]

oui,
c'est ça.

Ensuite on a ou
donc ...

[Jihane89]

:triste: ?

[Sve@r]

:triste: ?

Fais un effort aussi quoi !!! Tu veux qu'on te fasse tout ?
x²+2xy+y² ça ne te dit rien ?