Convergence d'une suite

[mehdi-128]

Bonjour je bloque sur cet exercice :

1) La suite définie par :

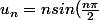est elle convergente ?

Je dirai non mais je suis pas sur ...

2) On suppose qu'une suite ( ) soit telle que aussi grand soit A, il y ait des termes de cette suite supérieurs à A.

En utilisant la suite du 1) peut on dire que la suite ( ) diverge nécessairement vers

La je sais pas du tout ...

Merci

[MacManus]

Bonjour.

saurais-tu dire les valeurs que prennent , pour ??

[mehdi-128]

Bonjour.

saurais-tu dire les valeurs que prennent , pour ??

est compris entre -1 et 1 ...

[MacManus]

oui les valeurs vont toujours osciller entre -1 et 1 pour tout n (les valeurs prises sont même -1, 0 et 1), donc en déduit que la suite n'admet pas de limite finie.

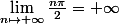
Sinon, on peut dire que , et par continuité de la fonction sinus sur R, on en déduit que la suite n'admet pas de limite finie, et est donc divergente.

[mehdi-128]

oui les valeurs vont toujours osciller entre -1 et 1 pour tout n, donc en déduit que la suite n'admet pas de limite.

Ah d'accord merci. Et pour la question 2 aurais tu une petite idée ? Je dirai non vu qu'elle n'a pas de limite

[Purrace]

tu vient juste de voir que la suite osciller a chaque pas dans le positif et negatif donc

[MacManus]

Formellement, on a :


en particulier, cette suite n'est pas bornée !
or, si la suite est bornée, le fait de multiplier par n, "casse" la bornitude. On peut trouver un rang N à partir duquel tous les termes de le suite seront > A pour n > N. Ce qui est bien la définition d'une suite divergente.

[mehdi-128]

Formellement, on a :


en particulier, cette suite n'est pas bornée !
or, si la suite est bornée, le fait de multiplier par n, "casse" la bornitude. On peut trouver un rang N à partir duquel tous les termes de le suite seront > A pour n > N. Ce qui est bien la définition d'une suite divergente.

Pour moi elle ne peut pas diverger vu qu'elle va osciller entre -n et n ...

[MacManus]

Oui jme suis un peu embrouillé.

mais le fait qu'elle oscille entre -n et n ne change rien, pour tout n, elle n'admet pas de limite finie.

[mehdi-128]

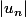
Oui jme suis un peu embrouillé. Jpensais à la suite en fait.
qui tend vers lorsque n tend vers , mais ça n'a aucun intérêt !

mais le fait qu'elle oscille entre -n et n ne change rien, pour tout n, elle n'admet pas de limite finie.

D'accord merci....

[MacManus]

Pour montrer que la fonction sinus n'admet pas de limite, on peut raisonner par l'absurde en supposant que la fonction sinus converge vers une limite finie L. En utilisant les deux suites extraites et , on montre que L = 0 = 1. Or il y a unicité de la limite, donc contradiction. Sinon on peut aussi utiliser des formules de trigo.

[mehdi-128]

Pour montrer que la fonction sinus n'admet pas de limite, on peut raisonner par l'absurde en supposant que la fonction sinus converge vers une limite finie L. En utilisant les deux suites extraites et , on montre que L = 0 = 1. Or il y a unicité de la limite, donc contradiction. Sinon on peut aussi utiliser des formules de trigo.

Ah ça c'est car 2 suites extraites admettent la même limite ? On fait la limite lorsque n->0 ?

[MacManus]

oui, deux suites extraites d'une suite convergente admettent la même limite.
non, on fait tendre n vers l'inifini.