Bonjour,
J'ai un problème pour cet exercice car je ne sais pas quelles propriétés utiliser.
(C) est un cercle de centre O et de rayon 2.
Soit A un point de(C) et I le milieu de [OA]. La médiatrice de [OA] reocupe (C) en B et C.
1) Montrer sue AOB=AOC=60°
2) Montrer que OBAC est un losange.
3) Calculer BC.
Merci d'avance pour votre aide.
Géométrie : losange dans un cercle
2 messages
- Page 1 sur 1
salut armain voila une methode
1)
on a
*OB=OC (car B et C sont ds la cercle dont le centre est O)
*OI=OI
*IB=IC (en utilisant les 2 points precedants+pythagore)
donc les 2 triangles OBI et OCI sont isometriques
dont les angles correspondantes sont =
cad IOB=IOC et OIB=OIC et OIB=OIC
en plus on a cos(AOB)=cos(IOB)=IB/OB=1/2=cos(60)
donc AOB=60(car AOB et >0)......
2)il suffit de mq * OB =BA= AC= CO
* (BC) est perpendiculaire a (OA)........
3)plusieures methodes...
par expl
BC=2*BI
pythagore appliqué au triangle OBI--->BI=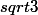
d'ou BC=2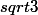
1)
on a
*OB=OC (car B et C sont ds la cercle dont le centre est O)
*OI=OI
*IB=IC (en utilisant les 2 points precedants+pythagore)
donc les 2 triangles OBI et OCI sont isometriques
dont les angles correspondantes sont =
cad IOB=IOC et OIB=OIC et OIB=OIC
en plus on a cos(AOB)=cos(IOB)=IB/OB=1/2=cos(60)
donc AOB=60(car AOB et >0)......
2)il suffit de mq * OB =BA= AC= CO
* (BC) est perpendiculaire a (OA)........
3)plusieures methodes...
par expl
BC=2*BI
pythagore appliqué au triangle OBI--->BI=
d'ou BC=2
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 147 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
