[CORRIGÉ DISPONIBLE À LA FIN, MERCI]
Bonjour je viens de commencer le collège en Sciences de la Nature (anciennement Sciences Pures) et bah, j'ai vraiment de la difficultée en math...
1er et deuxième cours le prof explique comment trouver le zéros dans des fonctions (la plus difficile étant):
3x+1
______________
(x-1)(2x+3)(x+1)
On doit trouver c'est quelle fonction:
Rationnelle (jusque là c'est pas bien compliqué)
ensuite on doit trouver le domaine:
IR sauf contraintes: déno = 0
______________
(x-1)(2x+3)(x+1)
Donc les contraites sont:
1, -1.5 et -1
donc le domaine =
IR \ { -1.5 , -1 , 1 }
Et on doit pour finir trouver le zéros:
y = 0
0 = 3x+1
______________
(x-1)(2x+3)(x+1)
on envoie tout ce qui est en bas * le 0
0 = 3x+1
-1 = 3x
__ __
3 3
x = -1
Bon, ça c'est le plus compliqué qu'on a appris en classe! Et j'avais déjà un peu de difficultée.
Le prof nous donne un document et nous demande de le faire pour lundi (y a 4 pages je crois) et bah, c'est chaud!
J'aurai besoin d'aide pour:
1. d) h(x) = ( 5x - 8x² ) ( 15x³ - 7x ) ^1/3 (exposant 1/2 quoi).
J'aimerai savoir pourquoi c'est pas une fonction polynomiale et:
c) g(t) = ( 4t³ - 7t )³ ( 5t - 8t² )
C'est une polynomiale selon le corrigé et j'aimerai savoir comment trouver son degré.
J'ai une autre question:
2. Déterminer les zéros des fonctions suivantes.
a) f(x) = 4x³ - 2x²
Faut trouver les zéros
et la b) g(x) = 8 ( 2x + 1 )³ ( 3x - 2 )^5 + 15 ( 2x + 1)^4 ( 3x - 2 )^4
Donc on trouve les zéros comment? J'ai vraiment aucune idée et je suis vraiment désesperé. Je capte rien, j'ai pris des cours de rattrapage, mais c'est pas encore commencé en fait.
ensuite y aurait celle-là:
c) f(t) = t³ + 7t² - 3t - 21
Elle a pas l'air bien compliquée, mais je bloque. C'est tout je bloque j'ai vraiment de la difficultée en math.
et d) f(x) = \/¯ ( 15x^5 - 75x³ + 60x )
Et une autre qui pourrait me poser probablement problème:
4. Déterminer le domaine des fonctions suivantes:
c) h(x) = 1
____________ + \/¯ ( 5x - 12)
\/¯ ( 10 - 2x)
aussi:
e) f(x) = \/¯ ( -6x² + x + 12 )
et:
f) k(x) = 8\/¯ ( 3 - x )
_______
(x² - 1 )
y'aurait aussi:
7. Soit: f(x) = { x² - 1 si x < -1
3x + 5 si -1 < x < 4
7 si x = 4
5 - 3x² si x > 4 et x =/= 7
et là on demande:
Évaluer, si possible:
a) f(-5)
c) f(0)
f) f(7)
J'ai rien compris à la question en fait...
Ça veut dire quoi évaluer? et même en sachant ça veut dire quoi je ne saurai le résoudre.
J'ai le corrigé si vous needez, mais moi ça m'est useless j'aimerai comprendre comment faire le problème
1. c) Oui (Degré 11)
2. a) 0 et 1/2
b) -1/2 , 2/3 et 1/54
c) -7 , \/¯3 et -\/¯ 3
d) 0, 2, -2, 1 et -1
4 c) domh = [ 12/5 , 5 [
e) domf = [ -4/3 , 3/2 ]
f) domk = [
7 a) 24
c) 5
f) non définie
Voilà, merci d'avance. J'aimerai qu'aucun modo ne modifie ou supprime mon post (sauf pour améliorer la lecture), car j'ai mis 1h pour l'écrire quand même. Et merci d'avance, c'est ma première fois sur votre forum ;)
Fonctions (Calcul Différentiel)
7 messages
- Page 1 sur 1
AlexhandreT a écrit:1er et deuxième cours le prof explique comment trouver le zéros dans des fonctions (la plus difficile étant):
3x+1
______________
(x-1)(2x+3)(x+1)
On doit trouver c'est quelle fonction:
Rationnelle (jusque là c'est pas bien compliqué)
ensuite on doit trouver le domaine:
IR sauf contraintes: déno = 0
______________
(x-1)(2x+3)(x+1)
Donc les contraites sont:
1, -1.5 et -1
donc le domaine =
IR \ { -1.5 , -1 , 1 }
Et on doit pour finir trouver le zéros:
y = 0
0 = 3x+1
______________
(x-1)(2x+3)(x+1)
on envoie tout ce qui est en bas * le 0
0 = 3x+1
-1 = 3x
__ __
3 3
x = -1
Bon, ça c'est le plus compliqué qu'on a appris en classe! Et j'avais déjà un peu de difficultée.
Pourtant la base de cette démo est sensée avoir été vue au primaire. A/B = 0 si A = 0 et B # 0. Que A s'écrive 3x+1 n'est qu'un détail...
AlexhandreT a écrit:J'aurai besoin d'aide pour:
1. d) h(x) = ( 5x - 8x² ) ( 15x³ - 7x ) ^1/3 (exposant 1/2 quoi).
J'aimerai savoir pourquoi c'est pas une fonction polynomiale et:
Une fonction polynomiale suppose des exposants entiers. Dans la mesure où t'as un exposant fractionnaire, ça devient une racine car
AlexhandreT a écrit: c) g(t) = ( 4t³ - 7t )³ ( 5t - 8t² )
C'est une polynomiale selon le corrigé et j'aimerai savoir comment trouver son degré.
C'est la valeur du plus grand exposant.
(4t³)³ * 8t² =
AlexhandreT a écrit:J'ai une autre question:
2. Déterminer les zéros des fonctions suivantes.
a) f(x) = 4x³ - 2x²
Faut trouver les zéros
et la b) g(x) = 8 ( 2x + 1 )³ ( 3x - 2 )^5 + 15 ( 2x + 1)^4 ( 3x - 2 )^4
Donc on trouve les zéros comment? J'ai vraiment aucune idée et je suis vraiment désesperé. Je capte rien, j'ai pris des cours de rattrapage, mais c'est pas encore commencé en fait.
Pour la première tu factorises par x². Pour la seconde, tu factorises par
AlexhandreT a écrit:ensuite y aurait celle-là:
c) f(t) = t³ + 7t² - 3t - 21
Elle a pas l'air bien compliquée, mais je bloque. C'est tout je bloque j'ai vraiment de la difficultée en math.
A la base c'est pas du niveau collège. La méthode ici est de trouver un zéro évident qu'on trouve en t=-7 (suffit d'un peu de flair en regardant -3t-21)
Donc maintenant on peut diviser ce polynôme par (t+7) ce qui donne f(t)=(t+7)(t²-3)
Et suffit de trouver les zéros pour t²-3 ce qui est assez évident vu qu'on peut écrire (t²-3) sous forme de produit remarquable (a²-b²) qui se factorise en (a-b)(a+b)
AlexhandreT a écrit:et d) f(x) = \/¯ ( 15x^5 - 75x³ + 60x )
Tu factorises par x. Ensuite tu poses X=x² et tu remplaces les x² par X puis tu trouves les zéros avec X. Ensuite, une fois que t'auras les X, tu remonteras facilement aux x.
AlexhandreT a écrit:Et une autre qui pourrait me poser probablement problème:
4. Déterminer le domaine des fonctions suivantes:
c) h(x) = 1
____________ + \/¯ ( 5x - 12)
\/¯ ( 10 - 2x)
Une dénominateur peut pas être nul. Et le nombre sous la racine peut pas être négatif. Ca te donnera la façon de calculer les x interdits. De là, tu remonteras le domaine de définition.
AlexhandreT a écrit:aussi:
e) f(x) = \/¯ ( -6x² + x + 12 )
et:
f) k(x) = 8\/¯ ( 3 - x )
_______
(x² - 1 )
Même méthode
AlexhandreT a écrit:y'aurait aussi:
7. Soit: f(x) = { x² - 1 si x 4 et x =/= 7
et là on demande:
Évaluer, si possible:
a) f(-5)
c) f(0)
f) f(7)
J'ai rien compris à la question en fait...
Ça veut dire quoi évaluer? et même en sachant ça veut dire quoi je ne saurai le résoudre.
Tu remplaces x par (-5) et tu calcules le résultat. Puis x par 0 puis par 7.
Salut,
bienvenu sur le forum!
L'exposant est 1/2 ou 1/3 ?
Dans les deux cas, ce n'est pas une fonction polynomiale parce que l'exposant n'est pas entier. Une fonction polynomiale est de la forme
 = a_nx^n+a_{n-1}x^{n-1} + ... + a_1x+a_0)
ce qui n'est pas le cas ici.
Pour qu'une fonction soit définie il faut que:
- son dénominateur ne s'annule pas
- si elle contient des racines carrées, il faut que ce qui est sous la racine oit positif.
Enfin, pour la dernière question, évaluer, ça signifie tout simplement calculer.
Sinon, essaye d'utiliser latex pour écrire proprement les formules (regarde le lien dans ma signature), et j'espère que ce post va t'aider
bienvenu sur le forum!
1. d) h(x) = ( 5x - 8x² ) ( 15x³ - 7x ) ^1/3 (exposant 1/2 quoi).
L'exposant est 1/2 ou 1/3 ?
Dans les deux cas, ce n'est pas une fonction polynomiale parce que l'exposant n'est pas entier. Une fonction polynomiale est de la forme
ce qui n'est pas le cas ici.
c) g(t) = ( 4t³ - 7t )³ ( 5t - 8t² )[/tex]
Le degré est la valeur de l'exposant le plus élevé une fois qu'on a tout développé.
Par exemple, le degré de 4t³ - 7t est 3.
Il n'est pas nécessaire de tout développer explicitement pour avoir le degré.
Dans, le terme de plus haut degré sera donné par
.
Dans la deuxième partie, le degré est donné par t².
Donc, le terme de plus haut degré du produit sera en ^
Le degré est donc 11.a) f(x) = 4x³ - 2x²
Faut trouver les zéros
La première étape est de factoriser; ici on voit que x² est un facteur commun et on a donc f(x) = x²(4x-2) = 2x²(2x-1)
f(x) s'annule pour x²=0 donc x=0 ou pour 2x-1=0 donc x=1/2
Les deux 0 sont donc 0 et 1/2.b) g(x) = 8 ( 2x + 1 )³ ( 3x - 2 )^5 + 15 ( 2x + 1)^4 ( 3x - 2 )^4
C'est la même idée, il faut commencer par factoriser. Ici, on voit que ( 2x + 1)^3( 3x - 2 )^4 est un facteur commun.c) f(t) = t³ + 7t² - 3t - 21
Celle là est moins facile. Il faut commencer par voir que -7 est une racine "évidente" f(-7) = 0 et ensuite factoriser par t+7.d) f(x) = \/¯ ( 15x^5 - 75x³ + 60x )
Il s'agit simplement de trouver les 0 de 15x^5 - 75x³ + 60x (la racine carrée ne change rien au problème)4. Déterminer le domaine des fonctions suivantes:
Pour qu'une fonction soit définie il faut que:
- son dénominateur ne s'annule pas
- si elle contient des racines carrées, il faut que ce qui est sous la racine oit positif.
Enfin, pour la dernière question, évaluer, ça signifie tout simplement calculer.
Sinon, essaye d'utiliser latex pour écrire proprement les formules (regarde le lien dans ma signature), et j'espère que ce post va t'aider
Bonjour,
pour la (1)
la fonction cube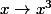
est une correspondance 1 pour 1 de dans
dans 
En anglais, "one-to-one mapping"
pour tout nombre y , il existe un unique nombre x tel que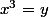
ce nombre est noté
exemple


pour la (7) le domaine de définition de la fonction
est la réunion de trois domaines
pour calculer f(x), il suffit de savoir dans quel domaine est situé x.
pour la (1)
la fonction cube
est une correspondance 1 pour 1 de
En anglais, "one-to-one mapping"
pour tout nombre y , il existe un unique nombre x tel que
ce nombre est noté
exemple
pour la (7) le domaine de définition de la fonction
est la réunion de trois domaines
pour calculer f(x), il suffit de savoir dans quel domaine est situé x.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
