Récurrence

par **Slack** » 25 Aoû 2010, 13:59

Soit :

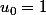
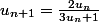
Je sais que

Je dois demontrer par rercurrence sur n que

Je prend un entier arbitraire p tel up verifie cela puis pour

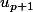
je remplace dans l'expression premiere de

et je tombe sur

et la je coince pcq c'est ca que l'on me demande.
(je dois sans doute me servir de la deuxieme forme mais je vois pas comment)

par **Olympus** » 25 Aoû 2010, 14:06

Je ne vois pas où est le problème ( à part que t'as fait une faute de frappe et que c'est

à la place de

) .

Ta récurrence me semble bonne ( manque un peu de clarté mais elle est bonne ) .

par **Finrod** » 25 Aoû 2010, 14:13

SI c'est bon quand tu remplaces n par n+1, n-1 devient n.

par **Slack** » 25 Aoû 2010, 17:17

Olympus a écrit:Je ne vois pas où est le problème ( à part que t'as fait une faute de frappe et que c'est à la place de ) .

Ta récurrence me semble bonne ( manque un peu de clarté mais elle est bonne ) .

Ah ok ma faute de frappe etait une erreur de calcul en realité d'ou la question. Merci

par **Slack** » 25 Aoû 2010, 20:38

Bon finalement j'ai refais le développement et je tombe sur

ce qui m'aide en rien. Si vous avez l'envie de refaire le petit developpement je suis preneur.

par **Finrod** » 25 Aoû 2010, 20:45

Slack a écrit:Soit :

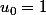
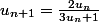
Je sais que
Je dois demontrer par rercurrence sur n que

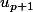
Je prend un entier arbitraire p tel up verifie cela puis pour je remplace dans l'expression premiere de et je tombe sur

Là tout ce qui est écrit est juste.

Et l'hérédité de la récurrence est bien démontrée.

par **Slack** » 25 Aoû 2010, 20:53

Ouai mais si

ca veux pas dire que

non?

par **Sa Majesté** » 25 Aoû 2010, 21:05

Slack a écrit:Ouai mais si ca veux pas dire que non?

Voir le post d'Olympus

par **Slack** » 25 Aoû 2010, 21:07

Sa Majesté a écrit:Voir le post d'Olympus

Mais euh c'est ce que je dis ce n'est une faute de frappe mais de calcul sauf qu'en recalculant je trouve ce qui affiché trois post plus haut d'ou la suite .

par **Finrod** » 25 Aoû 2010, 21:16

Slack a écrit:Ouai mais si ca veux pas dire que non?

Ben il y a une petite erreur, mais bon majorer

par

puis utiliser l'HR, ça fait même pas une ligne de calcul.

T'as juste oublier de diviser par deux un des termes.

par **Sa Majesté** » 25 Aoû 2010, 21:16

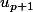
Slack a écrit:Je prend un entier arbitraire p tel up verifie cela puis pour je remplace dans l'expression premiere de et je tombe sur et la je coince pcq c'est ca que l'on me demande.

Alors tu as

Tu divises par 2 et tu ajoutes 1/6

d'où

par **Slack** » 25 Aoû 2010, 21:21

Ok pigé merci :zen:

Récurrence

Récurrence

Qui est en ligne