Limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ellhaym
- Membre Naturel
- Messages: 47
- Enregistré le: 17 Aoû 2010, 22:18
-
 par Ellhaym » 19 Aoû 2010, 21:59
par Ellhaym » 19 Aoû 2010, 21:59
Bonsoir, pourquoi
^n)
n'égale pas 0?
(n-1)/n étant inférieur à 1
Merci à vous :we:
-
oneil238
- Membre Naturel
- Messages: 23
- Enregistré le: 19 Aoû 2010, 19:31
-
 par oneil238 » 19 Aoû 2010, 22:01
par oneil238 » 19 Aoû 2010, 22:01
Parce qu'elle est égale à 1, je te conseil de factoriser ta fonction par n et de calculer pour vérifier.
EDIT: N'est plus valable avec le changement que tu as effectué.
-
Ellhaym
- Membre Naturel
- Messages: 47
- Enregistré le: 17 Aoû 2010, 22:18
-
 par Ellhaym » 19 Aoû 2010, 22:34
par Ellhaym » 19 Aoû 2010, 22:34
En fait la limite égale
)
C'est assez calculatoire (on doit passer par le log..) mais on trouve bien ça. Je voudrais seulement savoir pourquoi la limite ne vaut pas 0
Car une suite géométrique de raison comprise entre -1 et 1converge vers 0...non?
Mon erreur vient surement du fait que la raison varie selon les valeurs de n.
(Désolé Oneil j'avais oublié de mettre que c'était à la puissance n)
-
oneil238
- Membre Naturel
- Messages: 23
- Enregistré le: 19 Aoû 2010, 19:31
-
 par oneil238 » 19 Aoû 2010, 22:59
par oneil238 » 19 Aoû 2010, 22:59
Tu es sur de cette réponse, parce de plusieur manière j'obtiens 1 en valeur limite, et ne trouve pas d'erreur:
=e^(log((n-1)/n)^n)
=e^n*log((n-1)/n)
=(e^n)^log((n-1)/n)
Or lim en infini de log ((n-1)/n)=1
et log 1 =0
et donc (e^n)^0=1 non?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 19 Aoû 2010, 23:01
par Euler07 » 19 Aoû 2010, 23:01
Il faut effectuer un changement de variable. Remarque que tu peux simplifier ta fraction comme ceci :
^n)
-
Ellhaym
- Membre Naturel
- Messages: 47
- Enregistré le: 17 Aoû 2010, 22:18
-
 par Ellhaym » 19 Aoû 2010, 23:35
par Ellhaym » 19 Aoû 2010, 23:35
Ln(1-
^n)
=nLn(1-
)
=

ln(1+h) avec h=-1/n
=
}{h})
quand n tend vers +inf , (1/n) tend vers 0 d'ou
}}ln(1-(1/n))^n)
=
}}\frac{-ln(1+h)}{h})
or
}}\frac{ln(1+h)}{h})
=1
d ou
}}ln(1-(1/n))^n)
=-1 et donc:
}}(1-1/n)^n)
= exp(-1)
non?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 20 Aoû 2010, 00:40
par Euler07 » 20 Aoû 2010, 00:40
Bon raisonnement, pose plutôt
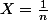
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 123 invités