Puissance fractionnaire

[Asterix]

Bonsoir, je bloque sur la détermination du domaine de définition (Df) d’une fonction puissance dont l’exposant est une fraction irréductible… Je suppose qu’il doit exister une théorème permettant de déterminer le Df de fonction(s) du type x^(p/q), p ;) ;) et q ;) ;)*, p/q irréductible.
Je sais que : x^(p/q) = (x^p)^(1/q) = (x^(1/q))^p mais comment savoir concrètement sur quel(s) Ensemble(s) la fonction est définie ? Exemple : x^(2/3), x^(-2/3), x^(5/6), x^(-5/6)
Je sais qu’il faut étudier si « p » (pair/impair/positif/négatif) et « q » (pair/impair/positif/négatif) mais existe-t-il une méthode simple applicable pour tout type de fonction de la forme x^(p/q) , p ;) ;) et q ;) ;)* (p/q irréductible) ?

Merci d’avance pour toute réponse…
Ps : Ce que je cherche avant tout c’est le théorème, s’il existe…

[COTLOD]

Bonsoir,
déjà il faut se rendre compte que l'entier ne pose aucune restriction. Ensuite à quelle conditions sur et peut-on calculer sachant qu'il s'agit de la racine q-ième ?

[Asterix]

Bonjour a tous (et Merci de t'être pencher sur la question CotloD),

Soit q ;) ;)*, q;)2
Si q est pair, D=;)+
Si q est impair, D=;)

Le problème étant le suivant :
la fonction racine n-ième, notée q;), est définie comme fonction réciproque de x^q sur [o ; +;)[.
Par conséquent les fonctions : x -> q;)x et x -> x^(1/q) sont identiques lorsque q est pair, mais différentes pour q impair, puisque dans ce cas, elles n’ont pas le même Domaine de Définition (Df)…

Mais ce n’est pas ce qui me pose problème.
Ma question est la suivante : S’il nous est donné, dans un exercice, une fonction du type x -> x^(p/q) , quelles sont les étapes par lesquelles il faut passer pour être certain de trouver – sans modifier la fonction - le véritable domaine de Df ?

Exemple :
1) x -> x^(4/3) = (x^4)^(1/3) = 3;)(x^4)
Et puisque x^4 ;) 0, Df = ;)
Alors comment se fait-il que lorsque l’on entre cette fonction dans la calculatrice, et que l’on demande la représentation graphique, celle-ci représente la fonction sur ;)+ ?
En l’occurrence, p=4 (si p était impair, cela changerait la donne, non ? Peux-tu me dire pourquoi « p ne pose aucune restriction » selon toi ?)

2) x-> x^(5/4) = (x^5)^(1/4) = 4;)(x^5)
Logiquement, ici Df = ;)+ que ce soit par la démonstration précédente ou par représentation graphique de la calculatrice…

Conclusion : Les fonctions : x -> q;)(x^p) et x -> x^(p/q) sont identiques lorsque p est impair, mais différentes pour p pair ?

Ma question finale est donc la suivante :
Soit x -> x^(p/q), p ;) ;) et q ;) ;)*, p/q irréductible.
Que faut-il faire pour être certain de déterminer Df sans modifier la fonction ?
Quelles sont les étapes à suivre dans l’ordre ? Doit-on commencer par regarder si p pair ? Ou q pair (puisque « p ne pose aucun restriction ») ?

Merci d’avance pour tte réponse.

Je cherche simplement à savoir ce qu’il faut faire dans l’ordre pour déterminer le Df et étudier une fonction du type x -> x^(p/q), p ;) ;) et q ;) ;)*, p/q irréductible.

[COTLOD]

ça y est, j'ai compris. En fait c'est plutôt une question de convention. Je viens de trouver un cours qui distingue les expressions et , la première étant définie sur 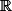et l'autre sur . La deuxième expression renvoie à la définition faisant intervenir le logarithme de qui n'est pas défini pour négatif (on ne se pose pourtant pas de question avec un exposant entier). Je suppose que la calculatrice utilise cette approche et ne cherche pas le plus grand domaine possible.

[COTLOD]

Pour répondre aux exemples je dirai (ce qui ne suit pas le cours dont je parle plus haut) :
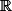1) le domaine est tant qu'on ne se place pas dans une famille de fonctions puissance, pourquoi se restreindre ?
1') le domaine est encore 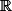car n'a pas besoin d'être positif pour en définir la racine cubique.
2) le domaine est .

[Nightmare]

Salut,

il y a pas grand chose à dire à part que la fonction est une bijection si q est impair mais n'induit une bijection seulement sur lorsque q est pair. Donc pour définir une réciproque, on a forcément à distinguer ces deux cas. Après, pour les questions de convention, c'est à toi de décider de les suivre ou non, mais si tu ne le fais pas, il faut évidemment le préciser.

[Asterix]

Ok, donc selon toi l'objectif est de déterminer le plus gd Df possible?
Et simple question sur la racine cubique, si ce qu'il y a sous le radical est négatif cela ne pose pas de pb? C'est certain? parce que si x-> x^(5/3) est définie sur R…
Alors sur quoi est définie x-> x^(6/5) ?

En tous cas mci d'avoir pris un peu de tps pour me répondre :)

[Asterix]

Donc il faut simplement que je précise au début de ma rédaction quelle méthode j'ai utilisé pour déterminer le Df de la fonction?

[COTLOD]

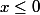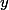Oui, le tout c'est que le correcteur ne pense pas que tu crois le logarithme défini pour . La racine cubique d'un négatif existe bien, par exemple , c'est l'unique réel qui vérifie .
Pour le domaine est toujours 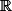. Je précise : tant que la fonction n'est pas prise dans une famille de fonctions puissances dont l'exposant serait amené à être irrationnel.

[Asterix]

Très bien.

Encore Merci pour vos conseils !