Récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 25 Juil 2010, 22:30
par Mathx » 25 Juil 2010, 22:30
Bonjour,
Comment peut on démontrer par récurrence sur n appartenant en N que :
k appartient à Z
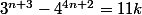
?
merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Juil 2010, 23:02
par Ben314 » 25 Juil 2010, 23:02
Salut,
la récurence n'est vraiment pas le moyen le plus adapté pour montrer ce genre de résultat, mais bon...
L'amorce ne pose pas de problème.
Pour l'hérédité, on suppose que, pour un certain entier n on a
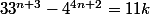
.
On a alors :
+3}-4^{4(n+1)+2}\ <br />=\ 3\times 3^{n+3}-256\times 4^{4n+2}\ <br />=\ 3\big(3^{n+3}-4^{4n+2})-253\times 4^{4n+2}\ <br />=\ \cdots)
je te laisse continuer...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 25 Juil 2010, 23:13
par Mathx » 25 Juil 2010, 23:13
Ok ! Donc on a : 3(11k)- 11(23*3^3n+3)= 11(3k-23*3^3n+3). On a une expression
de la forme 11k' ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Juil 2010, 23:19
par Ben314 » 25 Juil 2010, 23:19
C'est farfaitement ça...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 19:50
par Dinozzo13 » 26 Juil 2010, 19:50
j'approuve, Ben314, la récurrence ici peut-être facultative, mais étant donné qu'on nous y oblige, ce doit-être un exercice de 1re ou Tle S.
De manière analogue, cela revient à montrer que pour tout

:

est divisible par 11.
Tiens, je t'en donne un autre si tu veux réessayer :
Montrer que pour tout
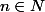
:

est divisible par 7.
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 20:35
par Mathx » 26 Juil 2010, 20:35
Ok ! Merci Dinozzo.
Facile pour l'amorce.
Pour l'hérédité, j'ai un truc du type :

Je pense que c'est égal à :
+6^{2n+2}+18^{n+1}=7(3^{2n+2}-2^{n+1})+36^{n+1}+18^{n+1})
Mais après... je vois pas :triste:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 20:56
par Dinozzo13 » 26 Juil 2010, 20:56
ok, j'vais t'aider un peu.
Il te faut montrer que
+2} -2^{(n+1)+1}=3^{2n+4}-2^{n+2})
est divisible par
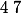
, après avoir supposé que pour tout

entier naturel,

est divisible par
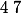
pour tout

.
Or d'après l'hypothèse, il existe un entier naturel
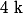
tel que :
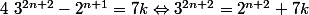
Par suite, on a :
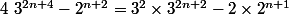
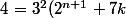-2\times 2^{n+1})
Je te laisse continuer :++:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:02
par Dinozzo13 » 26 Juil 2010, 21:02
J'en ai peut-être trop mis au début :ptdr:
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 21:04
par Mathx » 26 Juil 2010, 21:04
On aboutit à 7.2^{n+1}+7.9k =7(2^{n+1}+9k)
nn ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:08
par Dinozzo13 » 26 Juil 2010, 21:08
c'est exactement ça.
Pour t'en convaincre, pose
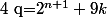
, tu obtiens donc
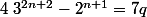
et par conséquent,

est bien multiple de
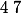
.
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 21:10
par Mathx » 26 Juil 2010, 21:10
Merci ;)
tu aurais un autre exercice stp pour m'entraîner sur le sujet ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:11
par Dinozzo13 » 26 Juil 2010, 21:11
Un petit dernier original ^^
Démontrer que pour tout entier naturel

non nul, il existe deux entiers
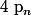
et
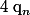
tels que :
^n=p_n+q_n \sqrt 3)
.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:25
par Dinozzo13 » 26 Juil 2010, 21:25
ah ben si tu en veux d'autres pour t'exercer, tiens :
Montrer que, pour tout entier naturel :
1°)

est un multiple de
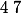
.
2°)

est divisible par
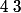
3°)

non nul,

4°)
^n\ge 1+na, a\in\mathbb{R}^*_+)
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 21:28
par Mathx » 26 Juil 2010, 21:28
Merci

Encore une fois, amorce simple !
Ensuite :
^{n+1}=2(2+\sqrt{3})^{n}=2.(p_n+q_n \sqrt{3})=(2p_n+3q_n)+\sqrt{3}(p_n+2q_n))
En posant :
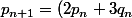)
et
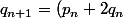)
, on a l'hérédité.
C'est juste ?
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 21:32
par Mathx » 26 Juil 2010, 21:32
Une autre question comme ça ;)
Existe-t-il des exos de récurrence de type problèmes ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:35
par Dinozzo13 » 26 Juil 2010, 21:35
:hum:
^{n+1}=(2+\sqrt 3)(2+\sqrt 3)^n)
-
Mathx
- Membre Naturel
- Messages: 62
- Enregistré le: 29 Déc 2009, 16:10
-
 par Mathx » 26 Juil 2010, 21:45
par Mathx » 26 Juil 2010, 21:45
Le reste est bon non ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:45
par Dinozzo13 » 26 Juil 2010, 21:45
Ben, je ne sais pas trop, mais il ne dois y avoir que des questions avec des récurrences dans ce problème alors.
un petit dernier :
1°) Montrer que pour tout entier naturel
)
est divisible par :
a) 2
b) 3
2°) Montrer que pour tout entier naturel
)
est divisible par 60.
3°) En déduire alors :
;n^2(n^4-1) \))
Edit : Si ton calcul est faux, alors le reste l'est surement.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Juil 2010, 21:47
par Ben314 » 26 Juil 2010, 21:47
Dinozzo13 a écrit:Il te faut montrer que
+2} -2^{(n+1)+1}=3^{2n+4}-2^{n+2})
est divisible par
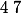
, après avoir supposé que
pour tout  entier naturel
entier naturel,

est divisible par
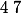
pour tout

.
Fait attention Dinozzo quand tu rédige une récurence. Lors de l'hérédité, on suppose que la propriété est vraie
pour un certain entier naturel n et il faut montrer qu'elle est aussi vraie pour
le suivant.
Si tu suppose que la propriété est vrai
pour tout entier n alors il n'y a plus rien à démontrer !!!! (et en plus, c'est qui "le" suivant de "tout entier" ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 26 Juil 2010, 21:54
par Dinozzo13 » 26 Juil 2010, 21:54
Nam, mais là je l'ai rédugé vite fait ^^
j'avais la flemme de tout bien taper ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 185 invités
, après avoir supposé que pour tout
entier naturel,
est divisible par
pour tout
.