DM sur variations et autres

[nono300010]

Bonjour,
voilà le début de mon DM:

Le problème est que ayant été malade (et l'étant encore) je n'ai pas pu avoir la méthode permettant d'effectuer ce devoir.
Merci de me guider. :happy3:

[gigamesh]

Bonsoir,
l'exercice fait partie de ce qu'on appelle l'analyse.
Pour étudier ta fonction coût total,
il s'agit :
* de calculer la fonction dérivée de C, notée C' (et qui dans le cas d'une fonction "coût total" s'appelle le coût marginal
* d'étudier le signe de cette dérivée
* d'en déduire les variations de C avec le théorème fondamental de l'analyse, qui est :
si f'>0 sur un intervalle I alors f est croissante sur cet intervalle I
si f'<0 sur un intervalle I, alors f est décroissante sur cet intervalle I

L'idée de base est que C' nous donne la vitesse à laquelle C croît, vitesse qui est négative lorsque C décroît...


Pour le calcul de C'(x),
il faut lire l'expression de C(x).
c'est une somme de trois termes
Dans ton cours, il est écrit que la dérivée d'une somme est la somme des dérivées. La formule est souvent écrite (u+v)' = u'+v'.
Donc nous allons dériver chacun des trois termes.
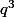
Le premier terme est ; sa dérivée est (c'est du cours, à connaître par coeur).
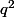
Le deuxième terme est ; on sait que la dérivée de est 2q (c'est dans le cours) ; et toujours dans le cours, la dérivée de -12 fois machin c'est -12 fois la dérivée de machin. La formule est (ku)'=ku' avec k une constante, ici k=-12.
Pour le troisième terme, 48q c'est de la forme mx+p donc c'est affine, avec m=48, la variable x qui ici s'appelle q, et p=0. Or le principe de base d'une fonction affine c'est qu'elle évolue toujours à la même vitesse, qui est justement le coefficient directeur de la droite qui représente cette fonction.

On se résume :


donc

Il reste à mettre 3 en facteur et à utiliser une identité remarquable.

Sans surprise, tu vas trouver que donc C est croissante (sans surprise car économiquement cela signifie que plus tu produis plus cela te coûte des sous...)