Moyenne arithmético-géométrique

par **cima** » 24 Fév 2010, 18:14

Bonjour,

laissez moi d'abord vous montrer l'énoncé de ce terrible exercice :

Bn+1= (An+Bn)/2

Les questions 3) 4)a et 4)b demeurent de véritables mystères pour moi...

Pour la 3) je bloque complètement sur l'hérédité de la récurrence en me retrouvant coincé avec des racines carrées des expressions de an+2 improbables, etc etc...

Pour la 4)a et b je n'ai aucune idée étant donné que je me retrouve constamment bloqué avec des racines bizarres, bref, je suis assez désespéré sachant que je ne sais plus trop quoi faire et que je viens de rédiger environ 20 pages de calculs compliqués et inutiles en fin de compte.

Merci d'avance de bien vouloir m'aiguiller.

Samuel.

par **Ben314** » 24 Fév 2010, 19:38

Salut,
Pour la 3), il faut effectivement faire une "petite" récurrence, mais en fait, pour démontrer que 0Ensuite, tu démontre l'une aprés l'autre chacune des 4 inégalités demandés.
Pour celles contenant des racines carrées, il te suffit délever au caré des dux cotés (deux nombres positifs sont dans le même ordre que leurs carrés).

La 4)a) se déduit de la 3) (sans nouveau calculs) puis de la définition de b(n+1)...

La 4)b) est une simple déduction du résultat de la 4)a) (par récurence)

par **cima** » 24 Fév 2010, 22:14

Okay, donc en gros pour l'hérédité, on doit prouver que :

0<an+1<an+2<bn+2<bn+1

Le seul endroit où ça coince, c'est pour an+2, doit on faire :

an+2=

(an+1 . bn+1)
an+2 =

( (;)an.bn) X (1/2(an+bn)) )

Et si tel est le cas en quoi cela prouve-t-il que :

an+1<an+2 ?

Je suppose qu'il faut développer an+2 mais j'ignore comment...

Merci encore pour votre aide précieuse.

Samuel.

par **Sa Majesté** » 25 Fév 2010, 18:23

Tu supposes

et tu cherches à montrer

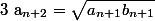
et

donc

Même philo pour montrer

Pour

, il suffit d'utiliser

par **cima** » 26 Fév 2010, 15:42

Merci beaucoup pour cette réponse, j'ai compris ! :id:

Juste une dernière chose, pour la question 4)b)
peut on considérer la suite (Vn) telle que :

Vn+1= An-Bn /2 ?

Etant donné que les suites sont adjacentes, je suppose qu'il faut prouver par la suite que

lim (bn-an) = 0
n-> +00

or je ne vois pas vraiment comment faire...

Merci encore.

par **Sa Majesté** » 26 Fév 2010, 19:51

cima a écrit:Merci beaucoup pour cette réponse, j'ai compris ! :id:

Juste une dernière chose, pour la question 4)b)
peut on considérer la suite (Vn) telle que :

Vn+1= An-Bn /2 ?

Si tu veux mais ce n'est pas nécessaire
Ça se prouve par récurrence

cima a écrit:Etant donné que les suites sont adjacentes, je suppose qu'il faut prouver par la suite que

lim (bn-an) = 0
n-> +00

or je ne vois pas vraiment comment faire...

C'est une conséquence de la question précédente

par **cima** » 26 Fév 2010, 20:05

C'est bon, j'ai compris pour la limite et la récurrence est quasiment réalisée donc tout va bien !

Merci encore une fois !!

Moyenne arithmético-géométrique

Moyenne arithmético-géométrique

Qui est en ligne