Division et congruence. Dm.

[Zorzor]

Hello, on a


Np =
et on veut prouver que divisible par 11
sachant que p=2q

Alors j'ai fais
10=1(11)
=1(11)
-1=0(11)
=0/9(11)
=0(11)
=0(11)

Est ce que on peut faire ca ? est ce qu'on a le droit de diviser ?

[nodgim]

Hello, on a


Np =
et on veut prouver que divisible par 11
sachant que p=2q

Alors j'ai fais
10=1(11)
Est ce que on peut faire ca ? est ce qu'on a le droit de diviser ?

10=-1 mod 11

[Zorzor]

ah oui, faute de frappe !
Mais après comme p=2q


vu que -1x-1 = 1

[Ericovitchi]

effectivement
10=-1 mod 11
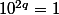
mod 11 c'est OK

Après oui tu a le droit de diviser que si c'est entier donc il faut juste démontrer en plus que est divisible par 9

[Zorzor]

ah oui d'accord ! merci beaucoup!
La suite est pas difficile après !

Merci encore.

[Nightmare]

4=0[4] et pourtant 4/2 n'est pas égal à 0/2=0 mod 4.

[Finrod]

Là ça marche mais il faut justifier : 9 premier avec 11

dans l'ex de nightmare -> 2 n'est pas premier avec 4.


De manière générale quand on divise un truc, x = 0 modulo n on divise aussi n i.e. x/p = 0[n/p]

(avec p qui divise x et n)

[Nightmare]

Oui, de toute manière pour pouvoir parler de division, il faut d'abord parler d'élément inversible.

[Zorzor]

pourquoi il faut prouver que 9 et 11 sont premier entre eux ?