Bonsoir à tous, je suis novice sur ce forum, et espère bien qu'il se revèlera d'une grande efficacité :)
J'ai trouvé cet exercice d'oral de l'ENS dans l'ODT, il est supposément abordable en sup, cependant je ne sais vraiment pas comment m'y prendre...
"Montrer que si n divise a^n - b^n alors n divise (a^n-b^n)/(a-b)"
Evidemment j'ai ramené le quotient à étudier à la somme qu'on obtient en factorisant an - bn par a - b (si quelqu'un sait comment noter les sommes sur ce site je suis preneur ) (je note an pour a^n...)
(an - bn) = (a-b)(somme k = 0 ---> k = n - 1 des a^(n-1-k)*b^k)
soit (a-b)(binome de newton jusqu'à n-1 sans les coefficients binomiaux)
Il faudrait donc demontrer que n divise cette somme, j'ai pensé à une eventuelle disjontion des cas selon le fait que n divise ou non (a-b), mais j'ai écarté cette idée, aucun des deux cas ne s'avérant plus simple, la factorisation par (a-b) dans le cas ou n divise a -b est faisable mais fais ressortir des termes de compensation qui si on les factorise font à leur tour ressortir des termes de compensation...
J'ai ensuite pris le probleme de maniere plus globale il faut montrer
(an - bn) = nq ==> (an -bn)(a-b) = nq'
et là franchement je sèche...
En esperant compter sur vous, merci bien !
Artihmétique - Theoriquement abordable en sup
14 messages
- Page 1 sur 1
Oui en effet, je pense que c'est abordable;
En posant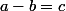 , développe
, développe
^n-b^n) . Tu trouves une expression où
. Tu trouves une expression où  est en facteur. Soit
est en facteur. Soit  un facteur premier de
un facteur premier de  .
.
Si ne divise pas
ne divise pas  , alors il divise l'autre facteur.
, alors il divise l'autre facteur.
Si divise
divise  dans l'autre facteur, tous les termes sont multiples de puissances de
dans l'autre facteur, tous les termes sont multiples de puissances de  , (donc divisibles par
, (donc divisibles par  ), sauf un qui est
), sauf un qui est  , mais aussi par hypothèse divisible par
, mais aussi par hypothèse divisible par  .
.
Faudrait regarder ensuite plus en détail ce qui se passe si est facteur multiple de
est facteur multiple de  , mais je te laisse le soin de conclure.
, mais je te laisse le soin de conclure.
En posant
Si
Si
Faudrait regarder ensuite plus en détail ce qui se passe si
Bonsoir,
Soit j'ai pas tout compris,... soit c'est un peu faux.
Soit j'ai pas tout compris,... soit c'est un peu faux.
Le nombre 6 divise 4x9, ne divise pas 4,... et ne divise pas non plus l'autre facteur...wserdx a écrit:Sine divise pas
, alors il divise l'autre facteur.
est tu bien sûr que, par exemple, 6 divise tout les coeff. binomiaux C(6,?) sauf un ( ces coeffs. sont 1, 6, 15, 20, 15, 6, 1...)wserdx a écrit:...des coefficients binomiaux tous divisibles par, sauf le coefficient de
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je pense que c'est juste mais... insufisant.
Si dans la décomposition de n en facteurs premiers il y a des carrés, ta preuve ne prouve pas que n divise (a^n-b^n)/(a-b)
Par exemple, si n=180=2².3².5, ta preuve montre seulement que 30=2.3.5. divise (a^n-b^n)/(a-b).
Ca peut peut être marcher en prenant q=p^k (plus grande puissance de p divisant n), en écrivant c=c'p^m (avec c' premier avec p) puis en évaluant les puissances de p qui apparaissent dans chaque terme de la somme (b+c)^n-b^n (une fois développée)...
Si dans la décomposition de n en facteurs premiers il y a des carrés, ta preuve ne prouve pas que n divise (a^n-b^n)/(a-b)
Par exemple, si n=180=2².3².5, ta preuve montre seulement que 30=2.3.5. divise (a^n-b^n)/(a-b).
Ca peut peut être marcher en prenant q=p^k (plus grande puissance de p divisant n), en écrivant c=c'p^m (avec c' premier avec p) puis en évaluant les puissances de p qui apparaissent dans chaque terme de la somme (b+c)^n-b^n (une fois développée)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ton idée marche peut être quand même.
On suppose que divise
divise ^n-b^n=\bigsum_{k=1}^{n}\left(\matrix{n\cr k}\right)c^k) et on veut montrer que
et on veut montrer que  divise aussi
divise aussi  .
.
Pour cela, il suffit de montrer que, pour tout (avec
(avec  premier et
premier et  ) apparaissant dans la décomposition en nombre premier de
) apparaissant dans la décomposition en nombre premier de  on a :
on a :  .
.
Si n'est pas divisible pas par
n'est pas divisible pas par  alors il est premier avec
alors il est premier avec  et comme
et comme  (car par hypothèse
(car par hypothèse  ) et
) et  on peut en déduire que
on peut en déduire que  c'est à dire que
c'est à dire que  .
.
Si est divisible par
est divisible par  , on peut essayer de voir si tout les termes de la somme
, on peut essayer de voir si tout les termes de la somme c^{k-1}) son bien divisiple par
son bien divisiple par  .
.
Comme est divisible par
est divisible par  , il suffit de montrer que
, il suffit de montrer que ) est divisible par
est divisible par  (avec l'hypothèse que n est divisible par
(avec l'hypothèse que n est divisible par  )
)
Cela semble... trés plausible...
On suppose que
Pour cela, il suffit de montrer que, pour tout
Si
Si
Comme
Cela semble... trés plausible...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, j'arrive à la même conclusion, et ce n'est pas si évident que ça à démontrer. J'ai vérifié le résultat expérimentalement pour un petit nombre de valeurs.
Je crois que pour finir il faut compter combien de fois apparait un facteur premier dans une factorielle (et ensuite dans un coefficient binomial)
Par exemple si est premier,
est premier,  apparait
apparait  fois dans
fois dans !)
Je crois que pour finir il faut compter combien de fois apparait un facteur premier dans une factorielle (et ensuite dans un coefficient binomial)
Par exemple si
C'est exactement ça.
Si tu veux un 'terme technique', le nombre de fois que le facteur apparait dans la décomposition d'un entier non nul
apparait dans la décomposition d'un entier non nul  s'appele la 'valuation p-adique' de
s'appele la 'valuation p-adique' de  et se note
et se note ) .
.
On a alors pour tout entier :
entier : =\bigsum_{k\geq 1}E\left(\frac{n}{p^k}\right)) où
où ) désigne la partie entière (la somme est en fait finie...)
désigne la partie entière (la somme est en fait finie...)
Cela donne en particulier ton résultat.
On peut aussi exprimer la valuation p-adique des coeff binomiaux et je pense qu'on peut vérifier que, si divise
divise  alors
alors  divise les coeff binomiaux
divise les coeff binomiaux ) pour
pour  .
.
Soit dit en passant, la méthode doit marcher, mais... je la trouve trés "laide" (c'est du gros bourrin) et je demande s'il n'y aurait pas plus simple (ou, plus "joli"), par exemple en utilisant l'indicatrice d'euler (sauf que je sais pas du tout si c'est vu en sup...)
Si tu veux un 'terme technique', le nombre de fois que le facteur
On a alors pour tout
Cela donne en particulier ton résultat.
On peut aussi exprimer la valuation p-adique des coeff binomiaux et je pense qu'on peut vérifier que, si
Soit dit en passant, la méthode doit marcher, mais... je la trouve trés "laide" (c'est du gros bourrin) et je demande s'il n'y aurait pas plus simple (ou, plus "joli"), par exemple en utilisant l'indicatrice d'euler (sauf que je sais pas du tout si c'est vu en sup...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
1) Si p est premier alors a^(p^k) = b^(p^k) mod p^k <=> a = b mod p.
2) Si p est premier et a^p - b^p = 0 mod p alors p divise (a^p - b^p)/(a-b).
Sachant ces deux résultats on peut résoudre le problème par récurrence :
C'est vrai si n=1.
On suppose que n divise a^n - b^n, et que n = p*m où p est premier.
En appliquant 2) sur a^m et b^m on en déduit que p divise (a^n - b^n)/(a^m - b^m)
On montre avec 1) et le théorème des restes chinois que m divise a^m - b^m.
L'hypothèse de récurrence avec m dit que m divise (a^m - b^m) / (a-b).
Donc n = p*m divise (a^n - b^n) / (a-b).
2) Si p est premier et a^p - b^p = 0 mod p alors p divise (a^p - b^p)/(a-b).
Sachant ces deux résultats on peut résoudre le problème par récurrence :
C'est vrai si n=1.
On suppose que n divise a^n - b^n, et que n = p*m où p est premier.
En appliquant 2) sur a^m et b^m on en déduit que p divise (a^n - b^n)/(a^m - b^m)
On montre avec 1) et le théorème des restes chinois que m divise a^m - b^m.
L'hypothèse de récurrence avec m dit que m divise (a^m - b^m) / (a-b).
Donc n = p*m divise (a^n - b^n) / (a-b).
Ne faudrait il pas que p et m soient premier entre eux ?Doraki a écrit:...p divise (a^n - b^n)/(a^m - b^m)...
...m divise (a^m - b^m) / (a-b)....
Donc p*m divise (a^n - b^n) / (a-b).
Sinon, l'idée me parrait bien plus jolie, et je pense que ça marche modulo le fait que :
a=p [mod p] => a^(p^k)=b^(p^k) [mod p^(k+1)]
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Le résultat est évident si n=p (premier). Il est pas trop dur si n=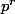 (mais là j'utilise le théorème d'Euler).
(mais là j'utilise le théorème d'Euler).
Ensuite on l'a par récurrence sur l'exposant :
si pour tout entier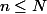 , on a l'implication voulue, on regarde le cas de l'exposant N+1; s'il est primaire c'est OK, sinon il s'écrit nm avec n et m premiers entre eux et
, on a l'implication voulue, on regarde le cas de l'exposant N+1; s'il est primaire c'est OK, sinon il s'écrit nm avec n et m premiers entre eux et 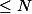 .
.
^m-(b^n)^m}{a^n-b^m}\times \frac{a^n-b^n}{a-b}) .
.
Le premier facteur est multiple de m par HR donc le premier membre aussi.
Symétriquement, il est multiple de n.
Donc il est multiple de N+1.
Ensuite on l'a par récurrence sur l'exposant :
si pour tout entier
Le premier facteur est multiple de m par HR donc le premier membre aussi.
Symétriquement, il est multiple de n.
Donc il est multiple de N+1.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 114 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
