Question de probabilités
13 messages
- Page 1 sur 1
Question de probabilités
Bonjour à tous,
Je viens de m'inscrire et j'ai une question à vous soumettre :
J'ai un système qui fonctionne de la manière suivante : toutes les x secondes (x serait de l'ordre de 1 à 1,5), un évènement se produit qui a une chance de 0.03% de déclencher un effet qui dure 10 secondes.
J'aimerais savoir comment calculer le pourcentage de temps (en moyenne) pour lequel l'effet sera actif. Je ne trouve pas de meilleure façon de poser la question donc je vais vous donner un exemple : (pour x = 1,5 s)
t = 0 -> l'effet ne se déclenche pas
t = 1,5 -> l'effet ne se déclenche pas
t = 3 -> l'effet se déclenche (il durera jusqu'à t = 13)
t = 4 / 5.5 / 6 / 7.5 / 9 / 10.5 -> l'effet ne se déclenche pas
t = 12 -> l'effet se déclenche à nouveau
t = 13.5 / 15 / 16.5 / 18 / 19.5 / 21 / 22.5 / 24 / 25.5 / 27 / 28.5 / 30 -> l'effet ne se déclenche pas
Sur mon exemple, l'effet a duré de t = 3 à t = 22 sur une durée totale de l'expérience de 30 secondes, soit un pourcentage "d'activité" d'environ 63% (19/30).
C'est donc ce pourcentage que j'aimerais calculer (ou au moins, connaitre) sur une très longue période (infinie, même, pour avoir une moyenne)
S'il vous est possible de m'expliquer le raisonnement derrière le résultat, je vous en serai d'autant plus reconnaissant, mais la valeur numérique (par exemple, pour x = 1.5 secondes) ou la formule permettant de calculer ce pourcentage en fonction de x me suffiraient.
Merci d'avance,
Bogdanov
Edit : Honte à moi, j'ai posé la question sans même avoir lu les règles du forum (trop impatient de connaitre la réponse), mais c'est fait désormais, et donc avant de quémander la réponse de votre part, je vous explique où mes recherches m'ont amené (sans résultat)
Je pensais obtenir une valeur approchée du pourcentage que je recherche (légèrement sur-estimée dans ce cas) en supposant qu'il suffisait de calculer, en moyenne, au bout de combien d'évènements l'effet se déclencherait.
La probabilité que l'évènement se déclenche au n-ième coup, sans s'être déclenché aux coups précédents, est (si je ne m'abuse) :
X(n) = 0.03 * 0.97^n
Et donc, en faisant un calcul d'espérance, en moyenne le nombre d'évènements nécessaires au déclenchement de l'effet serait :
Somme(de i = 1 à +infini) des X(n)*n
Cette somme semble converger vers 100/3 (33.333 quand je fais la somme de 1 à 1000 avec Excel) (100/3 étant l'inverse de 3/100, j'ai l'impression que je me suis un peu ridiculisé avec ma somme infinie alors qu'il aurait suffi de penser en physicien "période/fréquence" pour arriver à la même conclusion, mais passons... :ptdr: )
Donc il faudrait en moyenne compter sur un déclenchement de l'effet tous les 33.333 essais, soit 100 x / 3 secondes et si x = 1,5 alors, l'effet se déclencherait en moyenne une fois toutes les 50 secondes.
Et en divisant 10 par cette durée, j'obtiendrais une estimation du pourcentage que je cherche. L'effet serait donc actif 20% du temps. Estimation légèrement au-dessus de la réalité puisqu'il n'est pas impossible que deux fois, l'effet se déclenche de façon trop rapprochée pour bénéficier de deux fois 10 secondes de durée (comme dans mon exemple au début).
Comment obtenir le "vrai, bon résultat"?
Merci d'avance pour votre aide
Je viens de m'inscrire et j'ai une question à vous soumettre :
J'ai un système qui fonctionne de la manière suivante : toutes les x secondes (x serait de l'ordre de 1 à 1,5), un évènement se produit qui a une chance de 0.03% de déclencher un effet qui dure 10 secondes.
J'aimerais savoir comment calculer le pourcentage de temps (en moyenne) pour lequel l'effet sera actif. Je ne trouve pas de meilleure façon de poser la question donc je vais vous donner un exemple : (pour x = 1,5 s)
t = 0 -> l'effet ne se déclenche pas
t = 1,5 -> l'effet ne se déclenche pas
t = 3 -> l'effet se déclenche (il durera jusqu'à t = 13)
t = 4 / 5.5 / 6 / 7.5 / 9 / 10.5 -> l'effet ne se déclenche pas
t = 12 -> l'effet se déclenche à nouveau
t = 13.5 / 15 / 16.5 / 18 / 19.5 / 21 / 22.5 / 24 / 25.5 / 27 / 28.5 / 30 -> l'effet ne se déclenche pas
Sur mon exemple, l'effet a duré de t = 3 à t = 22 sur une durée totale de l'expérience de 30 secondes, soit un pourcentage "d'activité" d'environ 63% (19/30).
C'est donc ce pourcentage que j'aimerais calculer (ou au moins, connaitre) sur une très longue période (infinie, même, pour avoir une moyenne)
S'il vous est possible de m'expliquer le raisonnement derrière le résultat, je vous en serai d'autant plus reconnaissant, mais la valeur numérique (par exemple, pour x = 1.5 secondes) ou la formule permettant de calculer ce pourcentage en fonction de x me suffiraient.
Merci d'avance,
Bogdanov
Edit : Honte à moi, j'ai posé la question sans même avoir lu les règles du forum (trop impatient de connaitre la réponse), mais c'est fait désormais, et donc avant de quémander la réponse de votre part, je vous explique où mes recherches m'ont amené (sans résultat)
Je pensais obtenir une valeur approchée du pourcentage que je recherche (légèrement sur-estimée dans ce cas) en supposant qu'il suffisait de calculer, en moyenne, au bout de combien d'évènements l'effet se déclencherait.
La probabilité que l'évènement se déclenche au n-ième coup, sans s'être déclenché aux coups précédents, est (si je ne m'abuse) :
X(n) = 0.03 * 0.97^n
Et donc, en faisant un calcul d'espérance, en moyenne le nombre d'évènements nécessaires au déclenchement de l'effet serait :
Somme(de i = 1 à +infini) des X(n)*n
Cette somme semble converger vers 100/3 (33.333 quand je fais la somme de 1 à 1000 avec Excel) (100/3 étant l'inverse de 3/100, j'ai l'impression que je me suis un peu ridiculisé avec ma somme infinie alors qu'il aurait suffi de penser en physicien "période/fréquence" pour arriver à la même conclusion, mais passons... :ptdr: )
Donc il faudrait en moyenne compter sur un déclenchement de l'effet tous les 33.333 essais, soit 100 x / 3 secondes et si x = 1,5 alors, l'effet se déclencherait en moyenne une fois toutes les 50 secondes.
Et en divisant 10 par cette durée, j'obtiendrais une estimation du pourcentage que je cherche. L'effet serait donc actif 20% du temps. Estimation légèrement au-dessus de la réalité puisqu'il n'est pas impossible que deux fois, l'effet se déclenche de façon trop rapprochée pour bénéficier de deux fois 10 secondes de durée (comme dans mon exemple au début).
Comment obtenir le "vrai, bon résultat"?
Merci d'avance pour votre aide
Salut,
On peut modéliser de cette manière.
A chaque instant de temps, on attribue un indice .
.
Le premier instant s, prend l'indice 1
s, prend l'indice 1
L'instant s prend l'indice 2, etc...
s prend l'indice 2, etc...
On prend une variable aléatoire qui correspond à la durée de l'effet à partir de l'instant
qui correspond à la durée de l'effet à partir de l'instant 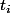 .
.
Cet effet dure entre et
et 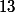 secondes.
secondes.
 si l'effet ne se déclenche pas, et
si l'effet ne se déclenche pas, et  si à l'instant
si à l'instant  l'effet se déclenche (
l'effet se déclenche (  )
)
On par exemple voir ca sous la forme d'un tableau
012x06xxxxx4xxx12xxxxxxxxxxx0
etc...
On va calculer la proba associée à notre variable .
.
 dépend de
dépend de 
Calcul de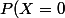)
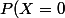=(1-p) = q)
 la proba que l'effet se déclenche,
la proba que l'effet se déclenche,  que l'effet se déclenche pas
que l'effet se déclenche pas
Calcul de)
Il faut que la variable de l'instant suivant ait une valeur différente de (l'effet se déclenche) et
(l'effet se déclenche) et
que nous nous déclenchions a l'instant
 = p \times P(X_{i+1} != 0) = p^2)
Calcul de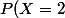)
Il faut que la variable à l'instant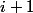 ne se déclenche pas
ne se déclenche pas
 = p \times (1-p) \times P(X_{i+2} != 0 ) = p(1-p)p=p^2q)
Calcul de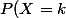)
=p^2q^{k-1})
Calcul de)
C'est la durée la plus longue de l'effet. Le tout est que personne ne se déclenche pendant la durée
de son effet
 = p q^{m-1})
On vérifie que notre somme de proba fasse bien 1 :
 + P(X=0)+P(X=m) = p^2 \frac{1 - q^{m-1}}{p} + q + pq^{m-1} = p + q = 1)
Ensuite, on va calculer l'esperance de notre variable aléatoire , qui représente la durée moyenne de l'effet
, qui représente la durée moyenne de l'effet
 = \bigsum_{k=0}^{m-2}kP(X=k) + mP(X=m))
Le calcul de la somme) donne
donne
 \\<br />S = p^2( \bigsum_{k = 0}^{m-2} q^k)' \\<br />S = p^2( \frac{1 - q^{m-1}}{q} )' \\<br />S = p^2( - (m-1)q^{m-2}q \ + \ 1 \times (1-q^{m-1})) \\<br />S = p^2( (1-m)q^{m-1} + 1 - q^{m-1}) \\<br />S = p^2( 1 - mq^{m-1} ))
Maintenant, on a fait toussa pour les temps discrets, mais en vrai, les variables durent pas 1,2,...secondes mais
 secondes
secondes
il parait alors judicieux de poser

(m représente le nombre d'instant)
pour s'arreter sur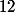 (dernier temps en seconde ou on peut se faire interrompre)
(dernier temps en seconde ou on peut se faire interrompre)
Puis on oublie pas de multiplier
Ce qui nous donne
)
On trouve alors notre espérance) :
:
 = S_2 + 13P(X=m) = S_2 + 13 \times pq^{m-1})
Enfin on remplace
 = S_2 + 13P(X=m) = 1.5 \times p^2( 1 - mq^{m-1} ) + 13 \times pq^{m-1})
En évaluent avec , on obtient :
, on obtient :
 = 0,30774) (secondes)
(secondes)
Pour un nombre assez grand d'instants, l'effet est en moyenne activée
}{n \times 1.5} = \frac{E_2(X)}{1.5} = 20,516%) (du temps)
(du temps)
Il faudrait simuler pour tester...
On peut modéliser de cette manière.
A chaque instant de temps, on attribue un indice
Le premier instant
L'instant
On prend une variable aléatoire
Cet effet dure entre
On par exemple voir ca sous la forme d'un tableau
012x06xxxxx4xxx12xxxxxxxxxxx0
etc...
On va calculer la proba associée à notre variable
Calcul de
Calcul de
Il faut que la variable de l'instant suivant ait une valeur différente de
que nous nous déclenchions a l'instant
Calcul de
Il faut que la variable à l'instant
Calcul de
Calcul de
C'est la durée la plus longue de l'effet. Le tout est que personne ne se déclenche pendant la durée
de son effet
On vérifie que notre somme de proba fasse bien 1 :
Ensuite, on va calculer l'esperance de notre variable aléatoire
Le calcul de la somme
Maintenant, on a fait toussa pour les temps discrets, mais en vrai, les variables durent pas 1,2,...secondes mais
il parait alors judicieux de poser
(m représente le nombre d'instant)
pour s'arreter sur
Puis on oublie pas de multiplier
Ce qui nous donne
On trouve alors notre espérance
Enfin on remplace
En évaluent avec
Pour un nombre assez grand d'instants, l'effet est en moyenne activée
Il faudrait simuler pour tester...
la vie est une fête 
Bonjour et merci pour votre réponse !
Il me semble que vous avez mal compris certaines données du problème :
la durée de l'effet, une fois qu'il s'est déclenché, n'est pas aléatoire, il dure toujours 10 secondes (à moins qu'il ne se déclenche à nouveau avant de s'être dissipé).
(en référence à votre phrase : "Cet effet dure entre 0 et 13 secondes.")
Ensuite, dans mon raisonnement, qui revient à dire : l'effet se déclenche en moyenne une fois tous les 33,33... coups ou toutes les 50 secondes, donc si on a de la chance et que l'effet ne se déclenche jamais "trop tôt" (c'est-à-dire avant qu'un effet précédent ne soit terminé), nous aurons exactement 10 secondes avec l'effet actif, toutes les 50 secondes.
Par conséquent, l'effet ne saurait être actif plus de 20% du temps. Je ne pense pas que la bonne réponse puisse être supérieure à 20%, à moins que je ne me trompe quelque part (ce qui est fort possible!)
Il me semble que vous avez mal compris certaines données du problème :
la durée de l'effet, une fois qu'il s'est déclenché, n'est pas aléatoire, il dure toujours 10 secondes (à moins qu'il ne se déclenche à nouveau avant de s'être dissipé).
(en référence à votre phrase : "Cet effet dure entre 0 et 13 secondes.")
Ensuite, dans mon raisonnement, qui revient à dire : l'effet se déclenche en moyenne une fois tous les 33,33... coups ou toutes les 50 secondes, donc si on a de la chance et que l'effet ne se déclenche jamais "trop tôt" (c'est-à-dire avant qu'un effet précédent ne soit terminé), nous aurons exactement 10 secondes avec l'effet actif, toutes les 50 secondes.
Par conséquent, l'effet ne saurait être actif plus de 20% du temps. Je ne pense pas que la bonne réponse puisse être supérieure à 20%, à moins que je ne me trompe quelque part (ce qui est fort possible!)
re,
La nuance : l'effet dure toujours 10 seconde, mais le temps actif qu'on comptabilise n'est pas toujours 10 seconde. Lorsque l'effet se déclenche au coup 5 et qu'il se declenche au coup 6, on considere que le premier effet est actif pendant la durée d'1 coup. D'ou la valeur de l'effet qui prend entre 0 et m, avec m a determiner
Apres je sais pas pourquoi j'ai pris 13 XD. m est censé représenter le nombre de coup ou est interrompu par un autre effet, dans ce cas là, m vaut 9/1.5 = 6
toujours est-il que jmetais planté : c'est pas m-2 sur la somme mais m-1.
Jreprends
 = \bigsum_{k=0}^{m-1} kP(X=k)+mP(X=m) \\<br />S = \bigsum_{k=0}^{m-1} kP(X=k) \\<br />S = p^2 \bigsum_{k=0}^{m-1} kq^{k-1} \\<br />S = p^2 ( \bigsum_{k=0}^{m-1} q^k )' \\<br />S = p^2 ( \frac{1-q^m}{1-q} )' \\<br />S = p^2 ( \frac{ -mpq^{m-1}+1(1-q^m)}{p^2} )' \\<br />S = -pmq^{m-1} + 1 - q^m \\<br />S = 1-q^{m-1}(q+mp))
On a alors, avec
 = 1.5 \times S + 10*P(X=m) \\<br />E_2(X) = 1.5 \times S + 10*p*q^{m-1} \\<br />E_2(X) = 1.5 \left( 1 - q^5(q+6p) \right) + 10 *p*q^5 \\<br />E_2(X) = 0.2763 \text{ (secondes) })
D'ou la durée moyenne de l'effet sur le laps de temps:
}{1.5} = 18,42%)
Au test, on trouve en moyenne entre et
et 
la durée de l'effet, une fois qu'il s'est déclenché, n'est pas aléatoire, il dure toujours 10 secondes (à moins qu'il ne se déclenche à nouveau avant de s'être dissipé).
La nuance : l'effet dure toujours 10 seconde, mais le temps actif qu'on comptabilise n'est pas toujours 10 seconde. Lorsque l'effet se déclenche au coup 5 et qu'il se declenche au coup 6, on considere que le premier effet est actif pendant la durée d'1 coup. D'ou la valeur de l'effet qui prend entre 0 et m, avec m a determiner
Apres je sais pas pourquoi j'ai pris 13 XD. m est censé représenter le nombre de coup ou est interrompu par un autre effet, dans ce cas là, m vaut 9/1.5 = 6
toujours est-il que jmetais planté : c'est pas m-2 sur la somme mais m-1.
Jreprends
On a alors, avec
D'ou la durée moyenne de l'effet sur le laps de temps:
Au test, on trouve en moyenne entre
la vie est une fête 
Salut,
Perso, je commencerait par regarder combien de "coup" dure "l'effet" sous la forme avec
avec  entier et
entier et  . Par exemple, s'il y a 1.5s entre chaque "coup" et que "l'effet" dure 10s, on a
. Par exemple, s'il y a 1.5s entre chaque "coup" et que "l'effet" dure 10s, on a  donc
donc 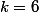 et
et  . Ensuite, en notant
. Ensuite, en notant  [=0.03] la proba. de déclanchement de l'effet et
[=0.03] la proba. de déclanchement de l'effet et 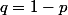 la proba de non déclenchement on a (en raisonant en terme de "coups" au dela du "coup" numéro k) :
la proba de non déclenchement on a (en raisonant en terme de "coups" au dela du "coup" numéro k) :
Proba. d'avoir l'effet sur ->
-> 
Proba. d'avoir l'effet sur ->
-> 
Donc proba. d'avoir l'effet à un moment aléatoire (au dela du coup k) :
+(1-\epsilon)(1-q^k)=1-q^k(1-\epsilon p)\) [= 0.183687]
[= 0.183687]
Sauf erreur, cela signifie qu'a long terme (à cause du fait que le raisonnement n'est valable qu'au dela du coup k), l'effet est actif en moyenne 18.3687% du temps.
Perso, je commencerait par regarder combien de "coup" dure "l'effet" sous la forme
Proba. d'avoir l'effet sur
Proba. d'avoir l'effet sur
Donc proba. d'avoir l'effet à un moment aléatoire (au dela du coup k) :
Sauf erreur, cela signifie qu'a long terme (à cause du fait que le raisonnement n'est valable qu'au dela du coup k), l'effet est actif en moyenne 18.3687% du temps.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
salut Ben314,
J'ai quelques questions parce que je comprends pas trop ta méthode:
Je crois comprendre que k représente un nombre de coups, et epsilone une fraction de nombre de coups (inférieure a 1)
Proba. d'avoir l'effet sur [n,n+\epsilon]\ -> \ 1-q^{k+1}
par contre, je ne comprends pas ce que représente n
J'ai quelques questions parce que je comprends pas trop ta méthode:
Je crois comprendre que k représente un nombre de coups, et epsilone une fraction de nombre de coups (inférieure a 1)
Proba. d'avoir l'effet sur [n,n+\epsilon]\ -> \ 1-q^{k+1}
par contre, je ne comprends pas ce que représente n
la vie est une fête 
n cet un nombre entier de coup quelconque (au dela du k-ième), c'est la même chose que "l'indice" de ton premier post.
Comme un "déclenchement" commence à un indice entier mais se termine à un "indice entier + ", pour qu'il n'y ait pas "d'effet" entre n et n+
", pour qu'il n'y ait pas "d'effet" entre n et n+ il faut (et il suffit) qu'il n'y ait pas eu de "déclenchement" sur les k+1 précédents indices entiers. Par contre, entre n+
il faut (et il suffit) qu'il n'y ait pas eu de "déclenchement" sur les k+1 précédents indices entiers. Par contre, entre n+ et n+1, il suffit de regarder les k précédents indices entiers....
et n+1, il suffit de regarder les k précédents indices entiers....
Comme un "déclenchement" commence à un indice entier mais se termine à un "indice entier +
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, je confirme m'etre planté!
Reste a trouver ou...
Edit : mauvais codeur.
Voila quelques résultats que j'ai :
p = 0.050000
maxTempo = 8
NDuree = 1000
NTest = 200
resultats
dureeMoyenneThFat = 0.23979
dureeMoyenneThBen = 0.22622
dureeMoyenneExperience = 0.23760; 0.23932
_________________
p = 0.030000
maxTempo = 10
NDuree = 1000
NTest = 200
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.16703
dureeMoyenneExperience = 0.18517;0.18353
Donc au final ma méthode a l'air correcte...
Rq : lorsque je fais sur une durée plutot courte, nos résultats sont au dessus de la dureeMoyenneExperience. (1 a 2%)
p = 0.030000
maxTempo = 10
NDuree = 200
NTest = 100
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.16703
dureeMoyenneExperience = 0.16273
Reste a trouver ou...
Edit : mauvais codeur.
Voila quelques résultats que j'ai :
p = 0.050000
maxTempo = 8
NDuree = 1000
NTest = 200
resultats
dureeMoyenneThFat = 0.23979
dureeMoyenneThBen = 0.22622
dureeMoyenneExperience = 0.23760; 0.23932
_________________
p = 0.030000
maxTempo = 10
NDuree = 1000
NTest = 200
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.16703
dureeMoyenneExperience = 0.18517;0.18353
Donc au final ma méthode a l'air correcte...
Rq : lorsque je fais sur une durée plutot courte, nos résultats sont au dessus de la dureeMoyenneExperience. (1 a 2%)
p = 0.030000
maxTempo = 10
NDuree = 200
NTest = 100
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.16703
dureeMoyenneExperience = 0.16273
la vie est une fête 
bon, ma méthode semble moins bonne que celle de Ben... (donc fausse probablement, mais ou?)
Voici qq tests effectués
p = 0.030000
maxTempo = 10
NDuree = 1000
NTest = 1000
q = 0.97000
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.18369
dureeMoyenneExperience = 0.18191
______________
q = 0.97000
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.18369
dureeMoyenneExperience = 0.18168
==============
maxTempo = 5
q = 0.97000
resultats
dureeMoyenneThFat = 0.096736
dureeMoyenneThBen = 0.096454
dureeMoyenneExperience = 0.096216
______________
q = 0.97000
resultats
dureeMoyenneThFat = 0.096736
dureeMoyenneThBen = 0.096454
dureeMoyenneExperience = 0.096181
==============
p = 0.10000
q = 0.90000
resultats
dureeMoyenneThFat = 0.29800
dureeMoyenneThBen = 0.29530
dureeMoyenneExperience = 0.29523
______________
q = 0.90000
resultats
dureeMoyenneThFat = 0.29800
dureeMoyenneThBen = 0.29530
dureeMoyenneExperience = 0.29418
==============
maxTempo = 20
q = 0.90000
resultats
dureeMoyenneThFat = 0.75523
dureeMoyenneThBen = 0.75429
dureeMoyenneExperience = 0.74606
______________
q = 0.90000
resultats
dureeMoyenneThFat = 0.75523
dureeMoyenneThBen = 0.75429
dureeMoyenneExperience = 0.74474
==============
maxTempo = 30
p = 0.20000
q = 0.80000
resultats
dureeMoyenneThFat = 0.98847
dureeMoyenneThBen = 0.98847
dureeMoyenneExperience = 0.97991
______________
q = 0.80000
resultats
dureeMoyenneThFat = 0.98847
dureeMoyenneThBen = 0.98847
dureeMoyenneExperience = 0.98038
==============
Deux tests sont effectués avec les même parametres, puis apres on change les parametres (delimitation avec des ====), et on reréalise deux tests.
edit:>boulzordoumesque<(?).
Bref, prendre la méthode de Ben314.
Voici qq tests effectués
p = 0.030000
maxTempo = 10
NDuree = 1000
NTest = 1000
q = 0.97000
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.18369
dureeMoyenneExperience = 0.18191
______________
q = 0.97000
resultats
dureeMoyenneThFat = 0.18420
dureeMoyenneThBen = 0.18369
dureeMoyenneExperience = 0.18168
==============
maxTempo = 5
q = 0.97000
resultats
dureeMoyenneThFat = 0.096736
dureeMoyenneThBen = 0.096454
dureeMoyenneExperience = 0.096216
______________
q = 0.97000
resultats
dureeMoyenneThFat = 0.096736
dureeMoyenneThBen = 0.096454
dureeMoyenneExperience = 0.096181
==============
p = 0.10000
q = 0.90000
resultats
dureeMoyenneThFat = 0.29800
dureeMoyenneThBen = 0.29530
dureeMoyenneExperience = 0.29523
______________
q = 0.90000
resultats
dureeMoyenneThFat = 0.29800
dureeMoyenneThBen = 0.29530
dureeMoyenneExperience = 0.29418
==============
maxTempo = 20
q = 0.90000
resultats
dureeMoyenneThFat = 0.75523
dureeMoyenneThBen = 0.75429
dureeMoyenneExperience = 0.74606
______________
q = 0.90000
resultats
dureeMoyenneThFat = 0.75523
dureeMoyenneThBen = 0.75429
dureeMoyenneExperience = 0.74474
==============
maxTempo = 30
p = 0.20000
q = 0.80000
resultats
dureeMoyenneThFat = 0.98847
dureeMoyenneThBen = 0.98847
dureeMoyenneExperience = 0.97991
______________
q = 0.80000
resultats
dureeMoyenneThFat = 0.98847
dureeMoyenneThBen = 0.98847
dureeMoyenneExperience = 0.98038
==============
Deux tests sont effectués avec les même parametres, puis apres on change les parametres (delimitation avec des ====), et on reréalise deux tests.
edit:>boulzordoumesque<(?).
Bref, prendre la méthode de Ben314.
la vie est une fête 
Salut fatal_error,
En utilisant ta méthode, si X désigne la V.A. désignant le nombre de "coups" que dure "l'effet", je pense que les différentes valeurs possibles pour X sont :
0,1,2,3,...,m,m+ où m+
où m+
Les proba. respectives de ces valeurs sont alors :

D'où une espérance=1-q^m(1-\varepsilon p)) (exprimée en "coups" alors que ton E2(X) est exprimé en secondes)
(exprimée en "coups" alors que ton E2(X) est exprimé en secondes)
Conclusion : c'est bien le même résultat que le mien et à mon avis, ton erreur porte seulement sur le "dernier terme" qui est m et pas m-1...
En utilisant ta méthode, si X désigne la V.A. désignant le nombre de "coups" que dure "l'effet", je pense que les différentes valeurs possibles pour X sont :
0,1,2,3,...,m,m+
Les proba. respectives de ces valeurs sont alors :
D'où une espérance
Conclusion : c'est bien le même résultat que le mien et à mon avis, ton erreur porte seulement sur le "dernier terme" qui est m et pas m-1...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
