Equations Differentielles

[Teta]

Bonsoir tout le monde, je poste mon problème car je suis bloqué sur un exercice... Alors voila :
1. Trouver une fonction g de la forme x --> a exp(-x) telle que pour tout réel x, on ait g'(x) + 3 g(x) = 2 exp(-x).
>> Donc la j'ai penser à la fonction qui a x --> (1/2) exp(-x)
2. Ensuite mon problème arrive: Démontrer qu'une fonction f est solution de l'équation (E): y'+3y=h, où h est la fonction telle que h(x)= 2 exp(-x), si et seulement si f-g est solution de l'équation de (E'): y'+3y=0

Et là je ne comprend plus grand chose, je tente des choses mais qui ne mène a rien... Merci d'avance pour votre aide.

[Mayor]

Salut.

Alors d'abord, ta fonction g n'est pas bonne... g'(x)=?

Ensuite pour 2., que penses tu si tu trouves une autre solution de (E), notée f, et que tu mets en regard tes deux equations : g'(x)+3g(x)=2exp(-x) et f'(x)+3f(x)=2exp(-x) ?
Elles se ressemblent.
Alors maintenant si je te dis "f-g", tu dois voir un lien avec ces deux équation...

Désolé, c'est pas très clair, mais c'est dur de te donner des indications sans te donner la réponse... :P

[Teta]

Salut.

Alors d'abord, ta fonction g n'est pas bonne... g'(x)=?

Salut merci de m'avoir aider, tu veut dire que la réponse à la 1 est fausse ?
Où veut-tu seulement dire que g'(x)=-3g(x)+2exp(-x) ?

Sinon pour la 2 je tente de comprendre je que tu essaye de me dire =)

[Mayor]

En effet, ta fonction g(x)=(1/2)exp(-x) ne fonctionne pas... Tu peux me donner sa dérivée stp?

Pour la deuxième question, un indice : "f - g"...

[Teta]

j'ai envie de dire que si g(x)= 1/2 exp(-x) alors g'(x)= exp(-x) non ? très grosse erreur ?

[Mayor]

Aïe... :marteau:


Alors,
Donc c'est pas bon...
Tu as quasiment la bonne fonction g, à un petit problème près...

[Teta]

comment as tu trouvée g'(x) ? désolé il est pas de bonne heure je suis plus très performant... je m'en excuse...

[dudumath]

si g(x)=a*f(x), alors g'(x)=a*f'(x)

[Mayor]

Ok, quand tu dérives, les constantes multiplicatives (ici ) ne sont pas modifiées.
Quand je dérive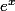 , j'obtient 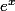, tout simplement.
Quand je dérive , le signe "-" sort, j'obtiens donc .
D'où, avec la constante ,

Dans ce cas là, tu as compris (j'espère) que ce qui pose problème, c'est le "-" qui sort lorsque tu dérives. Pour l'annuler, il suffit de mettre un "-" sur ton .

Je te demandes de dériver voir si tu as compris ce que je t'ai dit. Et ça répondra à ta première question...

[Teta]

D'accord, j'avais penser à la constante multiplicative mais pas au moins qui "sortait" donc si g(x)= (-1/2)exp(-x) alors g'(x)=(1/2)exp(-x)

[Mayor]

Effectivement, et donc,
Alors, , c'est toujours pas bon...

As-tu essayé la fonction qui est la plus simple à tester, c'est à dire avec a=1, maintenant que tu sais dériver comme il faut?