Equation differentielle linéaire

par **barbu23** » 26 Nov 2009, 02:24

Bonjour à tous :
Soit

une fonction numerique definie sur

par :

Je voudrais savoir quelle équation differentielle linéaire est satisfait par

?
Merci d'avance ! :happy3:

par **barbu23** » 26 Nov 2009, 12:08

Donc, on a :

c'est ça ? :happy3:

par **barbu23** » 26 Nov 2009, 20:56

Angélique_64 a écrit:Tu n'en es pas sûr?

Non, je suis sûr maintenant ! :happy3:

par **wserdx** » 26 Nov 2009, 21:14

Est-ce qu'on ne peut pas trouver une équation linéaire de plus petit ordre que 3?
je crois que

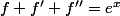
conviendrait aussi et est du second ordre.
Mais je ne vois pas d'équation simple du premier ordre. Quelqu'un en voit-il une?

par **bitonio** » 26 Nov 2009, 21:17

Je pense pas qu'il y en ai du premier ordre.

f''+f'+f=exp(x) est le plus simple je crois ... Cela se résout d'ailleurs sans trop de problème via equa cara et compagnie.

par **Ben314** » 26 Nov 2009, 22:59

Salut,
OUAIS, SUPER, GENIAL, j'en ai même trouvé une du premier ordre :

Je me demande même si en continuant mes (lourds) calculs, je n'arriverais pas à en trouver une d'ordre 0 :zen:

Equation differentielle linéaire

Equation differentielle linéaire

Qui est en ligne