lost-_- a écrit:Bonjour,
J'ai tellement besoin de votre aide!

Voilà une essai:
Pour la question 1)
Le moment de la force F est
M(F)= OM0^ F
= r ^ F
= r.er ^ -a/r3.er
= 0
Et on a la dérive du moment cinétique est égale au Moment de la force F
c-t-d
dL/dt = M(F)= 0
donc L=cte
=> L(t=0)= L(t)
=> OM0 ^ mv0= OM^ mv
=> OM ^ mv= (r0 . sin . v0 )ez
=> le plan (OM, v )est perpendiculaire à ez
=> le mouvement est plan.
Merci d'avance!!!
Exact pour la première partie. Pour la seconde, tu peux soit prouver que
 = \vec{0})
ou que
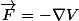
(V est, bien entendu, un champ scalaire). Les deux sont équivalents, vu que

.
Ca se fait de façont très facile avec la 2nde méthode; si tu ne te souviens pas de

en polaires, un petit changement de variable peut t'aider.
Pour le reste, je t'aiderais bien, mais il me faut d'abord trouver un équivalent de "diffusion" (je suis des cours en angleterre, et donc, bien évidemment, en anglais.)
Edition: \del donne un delta et non un del/nabla...

