Bonjour,
Comment simplifier le produit suivant ? :
(1-ab)(1-ab^2)(1-ab^3)...(1-ab^n)
Précision : c'est b seulement qui est élevé à la puissance, pas ab.
Grand merci d'avance pour votre aide.
Produit d'une suite
10 messages
- Page 1 sur 1
C'est ) ou
ou ) ?
?
sinon il y a un truc à essayer c'est faire ln f(a,b) =)
puis dériver f'a(a,b)/f(a,b) = formule qui se calcule assez facilement
formule qui se calcule assez facilement
(en dérivant/(1-q)) )
)
Après vous me direz, une fois qu'on a des formules pour f'a(a,b)/f(a,b) et f'b(a,b)/f(a,b) ça ne donne pas f(a,b) (mais ça donne df(a,b) =f'a(a,b)da+f'b(a,b) db). Peut-être qu'en intégrant en a,b on peut en déduire une formule ? qu'est-ce que vous en dites ?
sinon il y a un truc à essayer c'est faire ln f(a,b) =
puis dériver f'a(a,b)/f(a,b) =
(en dérivant
Après vous me direz, une fois qu'on a des formules pour f'a(a,b)/f(a,b) et f'b(a,b)/f(a,b) ça ne donne pas f(a,b) (mais ça donne df(a,b) =f'a(a,b)da+f'b(a,b) db). Peut-être qu'en intégrant en a,b on peut en déduire une formule ? qu'est-ce que vous en dites ?
Salut,
pour ma part, chui parti sur les polynômes, mais je trouve qqch de faux sans arriver a trouver l'erreur...
J'ai posé tel que :
tel que : (1-ab^2)...(1-ab^n))
( \frac{1}{a} - b^2)....(\frac{1}{a} - b^n))
(c-b^2)...(c-b^n))
avec
puis le polynome=a^n \bigprod_{i=1}^n (X-b^i )) , avec
, avec =u_n)
Ca ressemble à un polynome dont les racines sont les
je tente de trouver tous les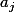 de
de  = \bigsum_{j=0}^{n} a_jX^j)
genre en évaluant en respectivement b^i pour tout i, je trouve=0) cqui va nous donner un système de n+1 équations à résoudre (en
cqui va nous donner un système de n+1 équations à résoudre (en 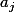 ) :
) :
^j = 0)
Du coup, jle mets sous forme matricielle :

La premiere matrice c'est une matrice genre vandermonde donc elle est inversible car) sont indépendants deux a deux du coup jpeux poser
sont indépendants deux a deux du coup jpeux poser

Et comme B vaut 0, X vaut 0 donc = 0) ce qui est faux.
ce qui est faux.
Mais ou est l'erreur?
pour ma part, chui parti sur les polynômes, mais je trouve qqch de faux sans arriver a trouver l'erreur...
J'ai posé
avec
puis le polynome
Ca ressemble à un polynome dont les racines sont les
je tente de trouver tous les
genre en évaluant en respectivement b^i pour tout i, je trouve
Du coup, jle mets sous forme matricielle :
La premiere matrice c'est une matrice genre vandermonde donc elle est inversible car
Et comme B vaut 0, X vaut 0 donc
Mais ou est l'erreur?
la vie est une fête 
fatal_error a écrit:Salut,
puis le polynome, avec
Ca ressemble à un polynome dont les racines sont les
je tente de trouver tous lesde
à partir de la; je ne comprends pas ce que tu fais ???
c'est quoi le rapport entre ces deux polynômes? (surtout pas le même!)
* In God we trust, for all others bring data *
Ben chui parti du principe qu'un polynome  = \bigsum_{k=0}^n a_k X^k) admet (mettons dans C) n racines simples et se factorise donc en
admet (mettons dans C) n racines simples et se factorise donc en =a_n \bigprod_i (X-\lambda_i))
Du coup à partir de=a_n \bigprod_i (X-\lambda_i)) , j'essaie de trouver les a_k tels que
, j'essaie de trouver les a_k tels que )
Supposons qu'on ait :
(X-4)) . Le polynome développé qu'on trouve est
. Le polynome développé qu'on trouve est  .
.
soit et
et 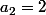
Maintenant en utilisant le même raisonnement qui plante :
 = 2(X-2)(X-4) = \bigsum_{k=0}^2 a_kX^k)

En fait, jme rends compte que je sais pas compter le nombre d'equation.
La dernière qui fait le lien, c'est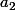 . On doit avoir
. On doit avoir 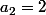 .
.
A partir de la, on obtient un systeme de n(=2) equations a n inconnues.
On peut donc avoir notre nouveau système :

D'ou on déduit de

Pour revenir a lexercice, on a alors :
}<br />\end{pmatrix}<br />\begin{pmatrix}<br />a_0 \\ .. \\ a_{n-1}<br />\end{pmatrix}<br />=<br />\begin{pmatrix}<br /> - a_nb^{n} \\<br />.. \\<br /> - a_n b^{n^2} \end{pmatrix})
avec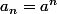
Apres, par contre, j'ai pas trouvé, j'ai abandonné les recherches, mais en gros, la matrice inverse d'une vandermonde, elle a des coeff avec des combinaisons (j'ose pas dire dérangements), et du coup, ca risque de faire des a_k relativement compliqués. Donc je pense pas qu'en développant ca simplifie l'expression :triste:
Du coup à partir de
Supposons qu'on ait :
soit
Maintenant en utilisant le même raisonnement qui plante :
En fait, jme rends compte que je sais pas compter le nombre d'equation.
La dernière qui fait le lien, c'est
A partir de la, on obtient un systeme de n(=2) equations a n inconnues.
On peut donc avoir notre nouveau système :
D'ou on déduit de
Pour revenir a lexercice, on a alors :
avec
Apres, par contre, j'ai pas trouvé, j'ai abandonné les recherches, mais en gros, la matrice inverse d'une vandermonde, elle a des coeff avec des combinaisons (j'ose pas dire dérangements), et du coup, ca risque de faire des a_k relativement compliqués. Donc je pense pas qu'en développant ca simplifie l'expression :triste:
la vie est une fête 
re,
Au secours !!! laisse les gens expérimentés ou toi même réfléchir deux seconds avant de te lancer à l'ordi.
(je ne te dis pas que je te donnerai une réponse car j'ai assez réfléchi et je ne trouve pas. mais j'en ai deja vu dure et qui sont résolu ici)
Jibse a écrit:Merci à vous tous. Je m'attendais à une réponse simple, mais je crois maintenant qu'il n'y en a pas. Je vais donc résoudre mon problème par la programmation.
Au secours !!! laisse les gens expérimentés ou toi même réfléchir deux seconds avant de te lancer à l'ordi.
(je ne te dis pas que je te donnerai une réponse car j'ai assez réfléchi et je ne trouve pas. mais j'en ai deja vu dure et qui sont résolu ici)
* In God we trust, for all others bring data *
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
