Belle équation à résoudre astucieusement

par **Timothé Lefebvre** » 28 Mar 2009, 10:29

Bonjour à toutes et à tous,

je vous propose ici une petite équation à première vue monstrueuse mais qui se rélève relativement simple à résoudre si l'on a un peu d'imagination

L'image suivante a été réalisée par Euler911 qui est parvenu à maîtriser le LaTeX pour la réaliser.

Voilà, désolé pour la taille de l'image !
Il s'agit de résoudre cette équation dans

Bon courage

PS : la dernière ligne c'est

[url="http://img18.imageshack.us/my.php?image=cd7b6ca3164f1c38a7db279l.gif"]

[/url]

par **Euler911** » 28 Mar 2009, 10:31

Bonjour,

...équation qui est équivalente à x²-x-1=0... nbre d'or et son conjugué!

par **Timothé Lefebvre** » 28 Mar 2009, 10:34

Ouaip

C'est effectivement ça, on tombe sur les deux racines réelles précisées.

par **Zweig** » 28 Mar 2009, 11:19

Salut,

Le nombre d'or et son conjugué sont solutions (on se ramène à

)

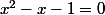
Un autre exercice sympa faisant intervenir les fractions continues :

Montrer qu'un couple

d'entiers naturels vérifie l'équation

si et seulement si

[CENTER]

[/CENTER]

avec

et

premiers entre eux et où le chiffre "2" apparaît

fois.

par **nodgim** » 28 Mar 2009, 16:35

Je croyais que, le nombre d'itérations étant limité, il fallait trouver la valeur exacte.. :cry:

par **Black_bird27fr** » 03 Avr 2009, 16:20

vu que le nombre est assé grand je préfére résoudre l'équation enétan une fraction continu qui va jusqu'a un nombre fini n de la
1-on remarque qu'en prenan le dernier terme (le plus bas) on a 1/(1+1/x)=x/x+1 le deuxiéme étape 1/(1+(x/(x+1))=(x+1)/(2x+1)...etc
2-on remarque qu'avec n étape on a ue suite Un tel que la fraction s'écrive sous la forme x=(Un-1 * x+U(n-2))/(Un * x +U(n-1))
3-cette suite numérique est défini par U0=1 et U1=1 et Un+2=Un+1 + Un ce genr de suite est di de deuxiéme ordre et sa resemble avec la suite de fiabonacci sauf pour le valeur de dépar qui son ché cette derniér 0 et 1 mais ce né pale sujet ce genr de suite est tré bien métrisé et on a Un= A*(d1)^n + B*(d2)^n avec d1 et d2 les solution de d^2-d-1=0 et A =(d2-1)/(d2-d1) et B=(d1-1)/(d1-d2)
4-et donc finalment tout ce qu'on a fair mtn cé de calculé combien d'étape il ya dan cette fraction qui sera pri pour un n et on aura l'équation x=(Un-1 * x+(n-1))/(Un * x +n) qui s'écri sous la forme d'un polynome de second degré
voila dsl pour l'écriture mé je suis encore nul question latex si ce né pa clair posé dé question.

par **Black_bird27fr** » 03 Avr 2009, 16:27

Zweig a écrit:Salut,

Le nombre d'or et son conjugué sont solutions (on se ramène à )

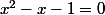
Un autre exercice sympa faisant intervenir les fractions continues :

Montrer qu'un couple d'entiers naturels vérifie l'équation si et seulement si

[CENTER][/CENTER]

avec et premiers entre eux et où le chiffre "2" apparaît fois.

on résoud ça grace a l'équation pell-fermat puis on fait une remarque sur la fraction p/q qui quand cé n étape tende ver l'infini elle ten ver racine de 2
voir cette page
http://villemin.gerard.free.fr/Wwwgvmm/Analyse/EquaPell.htm c'est assé simple et bien expliqué et pour avoir une idée plus dévelopé voir http://fr.wikipedia.org/wiki/%C3%89quation_de_Pell-Fermat

par **nodgim** » 03 Avr 2009, 16:29

Pardon, mais Latex ne corrige les fautes d'orthographe. Essaie de faire des efforts de ce coté là.

par **Black_bird27fr** » 03 Avr 2009, 16:35

le manque de mots aussi ^^

par **Zweig** » 03 Avr 2009, 16:36

Sauf que tu n'as rien montré du tout ... Elle est où l'équivalence ?

par **Black_bird27fr** » 03 Avr 2009, 16:39

équivalence comment ça ?

par **Zweig** » 03 Avr 2009, 16:42

"si et seulement si", on doit montrer une équivalence ... Tu remarques juste que la relation est une équation de Pell-Fermat (qui ne sert à rien ici au passage) mais sans donner de démonstration ...

par **Black_bird27fr** » 03 Avr 2009, 17:16

ah pour ça c'été juste une remaque pour la démonstration elle est assé simple regarde la premiére étape commence par remarqué que c'est bien racine 2 qui peu c'écrit de cette façon avec ça (je mé s2= racine de 2) 1+s2 - 1= 1+ 1/(s2 + 1) puis s2 +1 =2 +(s2-1) et donc s2 +1=2+ 1/(s2+1) et donc s2=1+s2 -1= 1+ 1/(2+1/(s2+1)) et la en refait la meme chose avec le nouveau s2+1 ce qui donne une serie infinie et bien sur aprés la remarque vien la démonstration il sufi de prendre Pn comme la proposition de la fraction jusqu'a n ave comme dernier terme s2+1 et on démontre avec la remarque que Pn+1 est aussi vrai (et on que P0 est vrai) donc la fraction est vrai pour n'importe quel étape n et donc vrai pour un dévelopment infinie
la seconde étape ets résultat de l'équation pell-fermat qui enféte conserne tout d entier qui n'est pas un carré parfait elle est donc comme cela x^2-dy^2=1 ce qu'on va démontrer la c'est qu' effectivement
1-si x et y sont solution alors x/y sera une approximation de racine de D en locurence 2 pour x^2-2*y^2=1 --(1)
démo: on a de (1)x/y - s2 = 1/(y^2 *( x/y +s2) qui est moindre que 1/(2*s2*y^2) et donc quand y devien plus grand x/y est de plus proche de racine 2 (s2) ce qui est le propre meme de l'approxiamtion
2- si x/y est une approximation qui vérifie x/y - s2 < 1/(2*s2*y^2) alors x et y sont des solutions a (1)
démo:x^2-2*y^2= y^2 *(x/y-s2)*(x/y+s2) qui est moindre que (1/2*s2)*(2*s2 + 1/(2*s2*y^2)
car x/y - s2 < 1/(2*s2*y^2) et donc y^2*(x/y-s2)< 1/(2*s2)
et x/y< 1/(2*s2*y^2) +s2
donc x/y + s2 < 1/(2*s2*y^2) +2*s2
et on que (1/2*s2)*(2*s2 + 1/(2*s2*y^2)<2 parceque 1/4y^2<1
pour finir on trouve que x^2-2*y^2 < 2 et supérieur a 0 (puisque on en pren que les solution positive alors puisque c'est un entier (x y et 2 le sont) il ne peut qu'etre 1 est donc x et y sont des solutions a (1) CQFD
(je suis mort sur le clavier lol)

par **nodgim** » 04 Avr 2009, 15:21

Black_bird27fr a écrit:le manque de mots aussi ^^

Certes mais c'est sûrement moins grave :ptdr:

par **Black_bird27fr** » 04 Avr 2009, 15:46

tu pense ? la défaillance sémantique est moin grave que les fautes d'orthographe.. et ben ou va le monde , mets en tête ce petite exemple un compliateur de programmation corrige toujours les fautes de syntaxes mais jamais les fautes sémantiques et tout le monde sais que le pc est une machine bête sans réel réflexion :stupid:
j'ai peur qu'il est une équivalence algébrique entre vous :ptdr:

par **nodgim** » 05 Avr 2009, 07:46

Black_bird27fr a écrit:tu pense ? la défaillance sémantique est moin grave que les fautes d'orthographe.. et ben ou va le monde , mets en tête ce petite exemple un compliateur de programmation corrige toujours les fautes de syntaxes mais jamais les fautes sémantiques et tout le monde sais que le pc est une machine bête sans réel réflexion :stupid:
j'ai peur qu'il est une équivalence algébrique entre vous :ptdr:

Le problème avec une orthographe pourrie est d'abord une réelle difficulté de lecture pour autrui: il faut d'abord repérer les sonorités avant de comprendre l'écriture.
Sijécrisansintaxeconprentonpluvitoumoinvitatoidevoirpourmoilechoièfai.

Quand l'orthographe est correcte, la lecture et la compréhension sont immédiates. Quand je dis que c'est plus grave pour toi, c'est que pour moi, il me suffira de me relire pour corriger les coquilles. Dans ton cas, si ton orthographe n'est que l'effet d'une négligence, ça sera facile à redresser. Par contre si, comme je le pense, c'est dû au fait d'une vraie défaillance des règles de français, la remise à niveau est plus difficile. Pas impossible à corriger certes, mais ce qui n'a pas été acquis en Primaire est bien difficile à rattraper plus tard. Cela dit, ça n'empêche pas les carrières scientifiques.

par **Black_bird27fr** » 05 Avr 2009, 17:40

nodgim a écrit:Le problème avec une orthographe pourrie est d'abord une réelle difficulté de lecture pour autrui: il faut d'abord repérer les sonorités avant de comprendre l'écriture.
Sijécrisansintaxeconprentonpluvitoumoinvitatoidevoirpourmoilechoièfai.

Quand l'orthographe est correcte, la lecture et la compréhension sont immédiates. Quand je dis que c'est plus grave pour toi, c'est que pour moi, il me suffira de me relire pour corriger les coquilles. Dans ton cas, si ton orthographe n'est que l'effet d'une négligence, ça sera facile à redresser. Par contre si, comme je le pense, c'est dû au fait d'une vraie défaillance des règles de français, la remise à niveau est plus difficile. Pas impossible à corriger certes, mais ce qui n'a pas été acquis en Primaire est bien difficile à rattraper plus tard. Cela dit, ça n'empêche pas les carrières scientifiques.

Tu dois surement parler de ton expérience personelle :ptdr: en racontant qu'il faut un effort supérieur quand on a pas une base au Primaire.Tu n'est pas obligé de comparer tous le monde a toi. :marteau:.
Et chapeau je vois que tu étais un professionnel du métier "Sijécrisansintaxeconprentonpluvitoumoinvitatoidevoirpourmoilechoièfai.'':doh:

Comme on dit : "chasse le naturel il revient au galop "^^.Moi j'aurais mis ça : Si jécri san sintaxe conpren ton plu vit ou moin vit a toi de voir pour moi le choi è fai (en plus même la tu mets des lettres en plus lol).

Ecoute c'est pas que je ne peut pas écrire correctement mais je ne trouve pas de différence a écrire "éléphant" ou "éléfan" :hum: "ph" c'est un ''f'' et ''t'' c'est pour la forme lol c'est un peut bête non ? et surtout a quoi cela pourais servir .C'est comme pour le vieux français : "veuillez vous ma gente dame vous assois sur ce modeste et humble blançois" :dodo: Comme disais mon prof tous ça pour dire : "veut-tu t'assoir sur cette chaisse ?" :zen:

Belle équation à résoudre astucieusement

Belle équation à résoudre astucieusement

Qui est en ligne