Dérivé partielle et champ de vecteur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mikelous
- Messages: 2
- Enregistré le: 11 Oct 2008, 16:02
-
par mikelous » 16 Mar 2009, 18:10
bonjour je vous demande de l'aide pour un petit exercice ou je suis bloquer:
soit
=(\frac{y}{x^2+y^2+z^2},\frac{-x}{x^2+y^2+y^2},0))
On me demande de montrer que
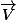
dérive d'un potentiel vecteur de la forme
)
Pour cela j'ai calculer le
=\frac{-2yx}{(x^2+y^2+z^2)^2}+\frac{2yx}{(x^2+y^2+z^2)^2}+0=0)
Donc je peut en déduire qu'il existe
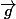
tel que
)
=(\frac{R}{dy}-\frac{dQ}{dz})\vec{i} + (\frac{dP}{dz}-\frac{dR}{dx})\vec{j} + (\frac{dQ}{dx}-\frac{dP}{dy})\vec{k})
je me retrouve avec trois équations:
PS: mon d=;) de la dérivé partielle. après ça je bloque si quelqu'un peut m'aider ce serai très aimable de sa part
-
mikelous
- Messages: 2
- Enregistré le: 11 Oct 2008, 16:02
-
par mikelous » 16 Mar 2009, 19:22
Personne a d'idée sur comment procédé ??
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
par kazeriahm » 16 Mar 2009, 20:19
Pour faire un d rond sous Latex c'est \dpart si je me rappelle bien
Sinon, si les composantes du vecteur g sont P, Q et R, regarde ce qui se passe quand P et Q sont nuls (on te demande de trouver U sous la forme (0,0,g)), ca devrait aller...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
