Dm sur les fonctions et dérivées 1ère S

[Clairedu21]

Bonjour,

J'ai un Dm à rendre jeudi prochain et j'aurais besoin d'un peu d'aide car certaines fonctions me posent problème. Voilà l'énoncé:

f est la fonction définie par: f(x)= x^3+3x^2+10x+5/ (x+1)^2

Elle est définie sur ]- l'infini; -1[U]-1; + l'infini[

Etudier les variations de f et dresser son tableau de variations.

En utilisant les formules de la dérivé u/v je tombe la dessus:

(3x^2+6x+10)(x+1)^2-2x+2(x^3+3x^2+10x+5)/((x+1)^2)^2

Après je ne vois pas comment simplifier pour avoir une fonction simple afin de construire son tableau de variation..

On considère f et g deux fonctions dérivables en a et définies sur R. On note fg la fonction définie par fg(x)=f(x)xg(x)
Démontrer que fg est dérivable en a et que (fg)'(x)=f '(x)xg(x)+f(x)xg'(x)

Indication: On pourra remarquer que fg(a+h)-fg(a)=fg(a+h)-f(a)g(a+h)-f(a)g(a)

Ici j'ai compris qu'il fallait utiliser la formule du taux d'accroissement f(a+h)-f(a)/h mais je ne vois vraiment pas comment l'utiliser..

Merci en tout cas d'avoir pris le temps de me lire et de m'aider à répondre à ces deux questions si vous le pouvez :we:

[Clairedu21]

S'il vous plait, vous n'auriez pas une petite idée? Car je bloque complètement sur ces deux questions, ce serait vraiment très gentil de votre part :briques:
Je vous remercie beaucoup de consacrer un peu de temps à mes problèmes! :)

[greg78]

Bonjour,

alors, déjà pour la première question, on peut presque dire que le plus dûr est déjà fait. Il ne reste qu'a déterminer le signe du numérateur selon les valeurs de x (le dénominateur est toujours positif). Pour ça, il faut développer l'expression, bidouiller un peu pour refactoriser en quelque chose de plus joli et puis après c'est immédiat.

Pour la deuxième, il faut en effet utiliser le taux d'accroissement.
Voilà rapidement comment on pourrait faire :

Soit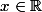 - {a}

On utilise que f est dérivable en a donc que et les limites des deux fractions qui donnent respectivement g'(a) et f'(a).

Voilà, j'espère que ca aidera.

[Clairedu21]

Merci greg78! J'ai effectivement trouvé le résultat de la première question donc c'est réglé :we: . Par contre pour la deuxième je ne comprends pas vraiment ta démarche car ce n'est pas vraiment le taux d'accroissement tel qu'on l'a vu en cours :cry: J'avoue que je suis en peu perdue..
Merci en tout cas d'avoir pris le temps de tout m'expliquer :happy2: