Dérivée de fonction puissance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
noursi93
- Messages: 7
- Enregistré le: 02 Jan 2009, 16:17
-
 par noursi93 » 02 Jan 2009, 16:18
par noursi93 » 02 Jan 2009, 16:18
bonjour,
qui peut m'aider à dériver cette fonction, je bloque complètement :
[(aX)^n]^m
aX est donc à la puissance n, le tout à la puissance m.
Merci de votre aide !!!
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2009, 16:20
par XENSECP » 02 Jan 2009, 16:20
^{n})^{m} = (aX)^{n.m})
cours de terminale

-
noursi93
- Messages: 7
- Enregistré le: 02 Jan 2009, 16:17
-
 par noursi93 » 02 Jan 2009, 16:27
par noursi93 » 02 Jan 2009, 16:27
oui c'est bien ce que je pensais mais le soucis c'est que ca ne correspond pas à ce qu'à fait le prof.
En fait je dérive une fonction de Cobb Douglas du type :
[(AlL)^(n-1/n)+AhH^(n-1/n)]^(n/n-1)
Et si je fais ce que vous me dite toutes les puissances se simplifient ??!!! ce qui ne peut pas marcher avec le résultat que je dois trouver.
-
mAroCaInEE
- Membre Relatif
- Messages: 266
- Enregistré le: 01 Jan 2009, 23:33
-
 par mAroCaInEE » 02 Jan 2009, 16:32
par mAroCaInEE » 02 Jan 2009, 16:32
C'est claire que:
^n)^m =(ax)^m*n)
Pour la derivée

n sait que
)^N]'=N*(F(x))'*(F(x))^(N-1))
alors tu vas l'apliquer sur ton exo
-
noursi93
- Messages: 7
- Enregistré le: 02 Jan 2009, 16:17
-
 par noursi93 » 02 Jan 2009, 16:35
par noursi93 » 02 Jan 2009, 16:35
c'est n+m ou n*m car on ne voit pas bien ?
-
mAroCaInEE
- Membre Relatif
- Messages: 266
- Enregistré le: 01 Jan 2009, 23:33
-
 par mAroCaInEE » 02 Jan 2009, 16:36
par mAroCaInEE » 02 Jan 2009, 16:36
c'est n*m désolée
-
noursi93
- Messages: 7
- Enregistré le: 02 Jan 2009, 16:17
-
 par noursi93 » 02 Jan 2009, 16:38
par noursi93 » 02 Jan 2009, 16:38
mais le problème c'est que tout se simplifier et que je trouve pas le résultat que je devrais trouver ...
-
mAroCaInEE
- Membre Relatif
- Messages: 266
- Enregistré le: 01 Jan 2009, 23:33
-
 par mAroCaInEE » 02 Jan 2009, 16:49
par mAroCaInEE » 02 Jan 2009, 16:49
pourquoi ce simplifie :doh: tu as bien
^n*m)
donc tu vas deriver par rapport au x donc tu vas sortir

car c'est une constante et tu vas appliquer la régle que je t'ai donné sur
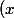^m*n)
-
noursi93
- Messages: 7
- Enregistré le: 02 Jan 2009, 16:17
-
 par noursi93 » 02 Jan 2009, 16:55
par noursi93 » 02 Jan 2009, 16:55
oui mais mes deux puissances se simplifient car c'est n-1/n et n/n-1 ...
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 02 Jan 2009, 16:58
par XENSECP » 02 Jan 2009, 16:58
Ta dérivée ce sera

-
mAroCaInEE
- Membre Relatif
- Messages: 266
- Enregistré le: 01 Jan 2009, 23:33
-
 par mAroCaInEE » 02 Jan 2009, 17:16
par mAroCaInEE » 02 Jan 2009, 17:16
Quand même il ne faut pas donner les solution comme ça!!!
Bon noursi93 comme je t'ai di a est une constante alors il faut la sortire de dérivée, puis tu vas prendre le X avec sa puissance qu'est m*n est appliqué tout simplement la régle de
^N]'=N.[f(x)]'.[f(x)]^((N)-1))
.
Dans ton cas tu as f(x)=x et N=n*m
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
