Besoin d'aide en trigo
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 26 Déc 2008, 18:19
par Chail » 26 Déc 2008, 18:19
Bonsoir,
J'ai à résoudre des équations trigonométriques, mais je n'y arrives pas, aps les cours qu'il faut...
Donc j'aimerais avoir un exemple de résolution pour cette équation:
sin3x = racine de 3/2
Merci d'avance
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 26 Déc 2008, 18:22
par guigui51250 » 26 Déc 2008, 18:22
il faut peut-être essayer avec un changement de variable. Pose X=3x, tu as donc sinX=racine de 3/2 donc tu en déduis les valeurs possibles pour X avec un cercle trigo. Et comme X=3x et que tu connais X, tu peux facilement trouver les différentes valeurs de x
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 26 Déc 2008, 18:24
par xyz1975 » 26 Déc 2008, 18:24
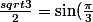)
On sait de plus que
=\sin(a))
équivaut à
 ou
ou 
avec
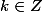
Ici X=3x
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 26 Déc 2008, 18:25
par guigui51250 » 26 Déc 2008, 18:25
xyz1975 a écrit: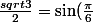)
euh je dirai plutot pi/3 et -pi/3
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 26 Déc 2008, 18:33
par xyz1975 » 26 Déc 2008, 18:33
guigui51250 a écrit:euh je dirai plutot pi/3 et -pi/3
Oui je me suis trompé en écrivant, merci.
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 26 Déc 2008, 18:42
par Chail » 26 Déc 2008, 18:42
Merci beaucoup
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 26 Déc 2008, 19:38
par Chail » 26 Déc 2008, 19:38
J'ai essayer de faire mon exo, voilà ce que ça donne:
sin3x=sin pi/3
3x=pi/3+2kpi
3x=pi-pi/3+2kpi
3x=pi/3+2kpi
3x=2pi/3+2kpi
x=pi/9+2kpi
x=2pi/9+2kpi/3
Pour la première équation:
*pour k=0 pi/9+2kpi = pi/9
*pour k=1 pi/9+2kpi = pi/9+2pi = 19pi/9 donc n'appartient pas à ]-pi;pi]
Pour la seconde équation:
*pour k=0 2pi/9+2kpi/3 = 2pi/9
*pour k=1 2pi/9+2kpi/3 = 2pi/9+2pi/3 = 2pi/9+6pi/9 = 8pi/9
*pour k=2 2pi/9+4pi/3 = 2pi/9+12pi/9 = 14pi/9 donc n'appartient pas à ]-pi;pi]alors sa mesure principale est 14pi/9-2pi = 14pi/9-18pi/9 = 4pi/9
*pour k=3 2pi/9 + 6pi/3 = 2pi/9+18pi/9 = 20pi/9 don n'appartient pas à ]-pi;pi] alors sa mesure principale est 20pi/9-2pi = 20pi/9-18pi/9 = -2pi/9
Les solutions sont:
S = {-2pi/9 ; 2pi/9 ; 8pi/9 ; -4pi/9 ; pi/9 }
Merci d'avance pour m'aider
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 26 Déc 2008, 20:26
par Huppasacee » 26 Déc 2008, 20:26
x=pi/9+2kpi
x=2pi/9+2kpi/3
attention il faut tout diviser par 3
tu as oublié de le faire pour la première ligne !
et , sache que tu peux aussi utiliser des valeurs négatives de k
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 26 Déc 2008, 20:38
par Euler911 » 26 Déc 2008, 20:38
Bonsoir
guigui51250 a écrit: xyz1975 a écrit: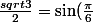)
euh je dirai plutot pi/3
et -pi/3
:doh: ?!

!!!

-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 26 Déc 2008, 20:56
par guigui51250 » 26 Déc 2008, 20:56
oups sorry, là c'est de la grosse boulette...
pi/3 et 2pi/3 ça va mieux
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 26 Déc 2008, 21:01
par Euler911 » 26 Déc 2008, 21:01
C'est
un peu mieux....
Je dirais plutôt

et

...
Mais bon:P
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 26 Déc 2008, 21:06
par Chail » 26 Déc 2008, 21:06
Huppasacee a écrit:attention il faut tout diviser par 3
tu as oublié de le faire pour la première ligne !
et , sache que tu peux aussi utiliser des valeurs négatives de k
Ah oui, merci
Sinon c'est justes ?
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 26 Déc 2008, 21:22
par Huppasacee » 26 Déc 2008, 21:22
S = {-2pi/9 ; 2pi/9 ; 8pi/9 ; -4pi/9 ; pi/9 }
cet ensemble de solutions a été calculé avec l'erreur de la première ligne
donc à revoir
Il devrait y avoir 6 solutions , à mon avis
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 26 Déc 2008, 21:36
par Chail » 26 Déc 2008, 21:36
OK merci je vais regarder ça
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 27 Déc 2008, 11:01
par Chail » 27 Déc 2008, 11:01
Il manquait bien une solution!
Juste une petite question, cos 0 = 1 ? C'est bien ça ?! En degré
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 27 Déc 2008, 11:07
par Chail » 27 Déc 2008, 11:07
Ah oui, il y a une équation qui me pose problème au départ, celle-ci
2cos x/3 - 1 = 0
A résoudre dans R
Merci d'avance
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 27 Déc 2008, 11:25
par guigui51250 » 27 Déc 2008, 11:25
Chail a écrit:Il manquait bien une solution!
Juste une petite question, cos 0 = 1 ? C'est bien ça ?! En degré
oui c'est bien ça :++:
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 27 Déc 2008, 11:28
par guigui51250 » 27 Déc 2008, 11:28
Chail a écrit:Ah oui, il y a une équation qui me pose problème au départ, celle-ci
2cos x/3 - 1 = 0
A résoudre dans R
Merci d'avance
alors pour celle-ci c'est le même principe :
2cos x/3 - 1 = 0
2cos x/3 = 1
cosx/3=1/2
tu pose X=x/3 puis comme tu connais ton cercle trigo tu peux facilement savoir pour quelles valeurs de X, cosX=1/2 donc tu en déduits les valeurs de x
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 27 Déc 2008, 11:28
par Chail » 27 Déc 2008, 11:28
Merci pour ta réponse
-
Chail
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2008, 15:31
-
 par Chail » 27 Déc 2008, 11:29
par Chail » 27 Déc 2008, 11:29
guigui51250 a écrit:alors pour celle-ci c'est le même principe :
2cos x/3 - 1 = 0
2cos x/3 = 1
cosx/3=1/2
tu pose X=x/3 puis comme tu connais ton cercle trigo tu peux facilement savoir pour quelles valeurs de X, cosX=1/2 donc tu en déduits les valeurs de x
Merci bien ! Je bloquais vraiment sur celle la
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
