Produit Scalaire et absurde

[Lolo6969]

Merciii ..

[Florélianne]

Bonjour,
Raisonner par l'absurde, ne veut pas dire être absurde ! seulement que supposer le contraire nous mène à une absurdité...
RAISONNER PAR L'ABSURDE :
On considère un triangle ABC non aplati
1) démontrer que, pour tout point M du plan : (Vecteur MA scalaire. Vecteur BC) + (vecteur MV scalaire. vecteur CA)+(vecteur MC scalaire . vecteur AB) = 0
pour simplifier l'écriture et rendre le problème plus agréable à lire, j'ai pris l'habitude de noter vecteur u : u*
il faut montrer que pour tout point M du plan :
MA*.BC* + MB*.CA* + MC*.AB* = 0
pour le démontrer par l'absurde, il faut donc partir du contraire :
Il existe un point M de plan tel que :
MA*.BC*+MB*.CA*+MC*.AB* n'est pas nul
Mais pour le moment je ne l'ai pas démontré... pas mon jour, migraine...
Bonne chance

[leon1789]

RAISONNER PAR L'ABSURDE :
On considère un triangle ABC non aplati
1) démontrer que, pour tout point M du plan : (Vecteur MA scalaire. Vecteur BC) + (vecteur MB scalaire. vecteur CA)+(vecteur MC scalaire . vecteur AB) = 0

C'est tellement facile de le faire de manière directe que je suis curieux de voir comment on s'y prend par l'absurde !

[Luc]

Salut,

Si tu raisonnes par l'absurdre, tu supposes qu'il existe un point M tel que , et tu veux arriver à une contradiction.

L'astuce ici est d'introduire le point A dans les vecteurs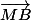 et 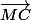. Développe les termes obtenus, les termes et se compensent, il te reste , ce qui est impossible ...

Remarque: Par symétrie, tu peux introduire B dans les vecteurs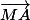 et 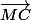, ou C dans les vecteurs 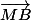et 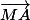, ça revient au même.

Luc

[Luc]

C'est tellement facile de le faire de manière directe que je suis curieux de voir comment on s'y prend par l'absurde !

Je suis assez d'accord avec toi, je trouve bizarre et pas très naturel de raisonner par l'absurde ici...

Luc

[Lolo6969]

Merciii pr le 1) c'est bouclé .. Mais pour la suite ça se complique !!

[aeon]

2a Supposons que les deux droites ne soient pas concourantes, elles sont donc parallèles, donc...

[Luc]

a) montrer que les droites (AA') et (BB') sont concourrantes

Moi c'est plutôt la que je raisonnerai par l'absurde :id: .

Raisonne par l'absurde et suppose que (AA') et (BB') ne sont pas concourantes.
Utilise le fait que les hauteurs sont perpendiculaires au côté opposé.

Et aboutit à une contradiction (Je te rappelle que le triangle n'est pas plat).

Luc

[leon1789]

Merciii pr le 1) c'est bouclé .. Mais pour la suite ça se complique !!

Je ne doute pas que tu l'as fait, mais peux-tu nous faire voir comment tu as rédiger (sans nous mettre les calculs intermédiaires) la preuve par l'absurde STP ?

[leon1789]

Je suis assez d'accord avec toi, je trouve bizarre et pas très naturel de raisonner par l'absurde ici...

Luc

Oui, et là, tu es gentil. Moi, je dirais même plus : c'est complètement "débile" (je pense à celui qui a fait l'énoncé, pas Lolo6969 évidemment) de faire un raisonnement par l'absurde pour cette question.

La réponse désirée est celle-ci :

On pose et supposons .
Maintenant calculons ...
On arrive à donc , ce qui est impossible car est supposé.
Conclusion : la supposition est fausse et est juste !

Que peut-on comprendre à ça ??? C'est absolument anti-pédagogique !!! Ca y est, je suis énervé............ :hum: :hum: :hum:

[leon1789]

b)Soit H le point d'intersection de (AA') et (BB'). En utilisant la 1er question, montrer que H appartient (CC').

et là aussi, je ne vois pas où est l'intérêt d'un raisonnement par l'absurde, vu c'est immédiat en utilisant le premier point. A moins qu'il faille un raisonnement par l'absurde pour dire que 0-0-0 = 0 :hum:

[Lolo6969]

Destressssse :) LooL
Mais c'est mon énoncé donc je ne sais quoi te dire !! :doh: :doh:
Merci pr le a) :)
et le b) je fais la meme chose ?

[leon1789]

Destressssse LooL
Mais c'est mon énoncé donc je ne sais quoi te dire !! :doh: :doh:

:zen:

et le b) je fais la meme chose ?

Mieux vaut (pour toi) faire plaisir à ton prof ... mais paraine-le pour qu'il vienne sur le forum , histoire de discuter de ça :ptdr:

[Lolo6969]

et tu pouurais m'aider ... enfin me donner des ptites pistes ?? Steuplai !! :)

[leon1789]

pour la dernière question :
(HA) est perpendiculaire à ..... ?
(HB) est perpendiculaire à ..... ?
ça te donne des produits scalaires nuls : lesquels ?
et ensuite , utilise la première formule avec les 3 produits scalaires (avec M=H)...

[Lolo6969]

J'aiiii pas compriiiis :)