Fonctions associées

[kalvy]

Voici un second problème, concernant cette fois-ci les fonctions associées.
Je n'ai répondu qu'à la 1ère question, n'étant pas sûre de la réponse à la seconde, et donc je me suis bloquée là ...

soit f, la fonction définie sur R par f(x) = x²+4x+3
1) Vérifier que pour tout x de R, f(x) = (x+2)²-1
Ca c'est bon, il suffit de développer f(x) et on trouve x²+4x+3

2) en déduire l'étude des variations de f.
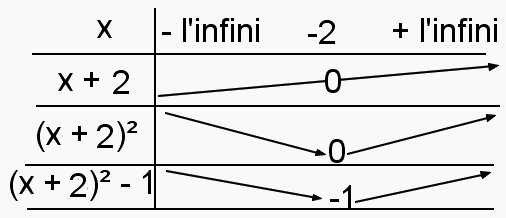
Ca c'est bon, aussi, en faisant la décomposition de la fonction, puis en regardant les signes de x+3 ; (x+3)² ; (x+3)-1, je trouve :

3) on considère un repère orthonormal (O, vecteur i, vecteur j), d'unité 1cm.
a. soit C la représentation graphique de f ans ce repère.
Déterminer les points d'intersection de C avec le axes des ordonnées.
b. Démontrer que la droite d'équation x=-2 est axe de symétrie de C.
c. Expliquer par quelles transformations géométriques onpeut déduire la courbe C de f de la parabole de référence P d'équation y = x²
d. Tracer la courbe c dans (o, vecteur i, vecteur j)

4) Tracer la droite D d'équation x - y + 3 = 0 et déterminer graphiquement l'ensemble S : S = {x réels tel que x²+4x+3 est inférieur ou égal à x+3}
Retrouver graphiquement la réponse à la solution de l'inéquation.

5) comparer les fonctions suivantes à la fonction f et justifier ainsi les constructions des courbes, à partir de celle de f. (Tracer les courbes de h, k, g et l dans 4 repères différents)
a. h telle que h(x) = x² - 4x +3
b. k telle que k(x) = -x² - 4x
c. g telle que g(x) = valeur absolue de (x²+4x+3)
d. l telle que l(x) = x² + 4(valeur absolue de x) + 3


Voilà, merci d'avance à ceux/celles qui pourront m'aider

[kalvy]

Personne ne peut m'aider pour ce problème ?

[Noemi]

Pour les coordonnées des points d'intersection avec les axes du repère, tu cherche les coordonnées des points de f qui vérifient y = 0 (axe des abscisses) et x = 0 (axe des ordonnées).

[kalvy]

Alors, les points d'intersection de C avec les axes du repèresont :
pour les abscisses : A(-3 ; 0) et A'(-1 ; 0)
pour les ordonnées : B(0 ; 3)

tu es d'accord, pour la rédaction aussi ?

[Noemi]

Pour la rédaction, il faudrait indiquer les calculs.

[kalvy]

Ah, le problème, c'est que je n'ai pas utilisé de calcul, mais j'ai juste regardé sur le graph'.
Alors, quel genre de calcul je dois faire pour trouver les coordonnées de ces points ?

[Noemi]

1) si y = 0, tu résous l'équation f(x) = 0
2) si x = 0, tu calcules f(0)

Je dois y aller, à ce soir peut être.

[kalvy]

Heu, je vais essayer
j'espère qu'on se reverra ce soir pour continuer, mon dm est à rendre pour mercredi, et j'y suis pas encore arrivée à bout .. Je vais essayer d'avancer le plus possible.
A tout a l'heure ^^

[kalvy]

Ca y est j'ai trouvé pour les calculs:

Pour x=0 :
f(x) = 0, donc :
(x+2)² - 1 = 0
(x+2)² - 1² = 0
(x+2-1)(x+2+1) = 0
(x+1)(x+3) = 0
x+1 = 0 ou x+3=0
x=-1 ou x=-3

donc, les points d'intersection de C et de l'axe des abscisses ont :
A(-1;0) et A'(-3;0)


pour y=0 :
f(x) = x²+4x+3
f(0) = 0²+4*0+3 = 3
donc, le point d'intersection de C et de l'axe des ordonnées est :
B(0;3)

Ca va comme explication ?


[en tout cas, les tiennes sont top ! j'y arrive bcp mieux avec tes explications ^^ :++: ]


Edit : j'en suis arrivée à la question 4. je te montre les réponses que j'ai fait jusque là pour voir si c'est correct :


1) on développe les fecteurs et on trouve le bon résultat
2) on trace le tableau de variations ( )
3) a. les calculs précédents
b. C est la représentation graphique de f. f étant décroissante sur ]-infini;-2] et croissante sur [-2;+infini[, l'ensemble de définition de f est donc centré en -2. don, la courbe de f est une parabole et la droite d'équation x=-2 est axe de symétrie de C.
c. on peut déduire la courbe C de f de la parable de référence p d'équation y=x², par une translation de vecteur : 3i-j.

4) à faire ^^
5) à faire ^^

voilà, donne moi ton avis quand tu repasseras


voici ma réponse à la question 4 :

4) les points M(-1;2) et N(1;4) sont 2 points de D, d'équation x-y+3=0. en effet, leurs coordonnées vérifient l'équation cartésienne :
-1-2+3=0 et 1-4+3 = 0
[on trace la droite sur le graph']
Pour la résolution graphique, de l'ensemble S, je ne sais pas comment faire ...

Pour la résolution de l'inéquation, je propose :
S={x de R / x²+4x+3 inférieur ou égal (<) x+3}
S={x de R / x²+4x+3-x-3 < 0}
S={x de R / x²+3x<0}
S={x de R / x(x+3)<0}
S={x de R / x<0 ou x+3<0}
S={x de R / x<0 ou x<-3}
S=]-infini ; -3]

je ne sais pas i c'est juste, je n'arrive pas toujours à savoir où changer le signe de l'inéquation quand il le faut ...

[Noemi]

L'ensemble est correct, sauf la fin pourquoi translation de vecteur 3i-j ?

[kalvy]

On a vu dans le cours :

"Soit a de R, et u une fonction,
alors, dans le repère (O,i,j), la courbe de la fonction u+a est l'image de la courbe de u par la translation de vecteur aj."

et

"Soit a de R, et u une fonction,
Alors, dans le repère (o,i,j), la courbe de la fonction f telle que f(x)=u(x+a) est l'image de la courbe de u par la translation de vecteu -ai".

Et, quand je regarde sur la calculette, la courbe de la fonction, je vois qu'elle est décalée de 3 unités de i, vers la gauche, donc de +3i, et d'une unité de j vers le bas, donc de -1j, d'où ma translation de vecteur : +3i-1j

C'est pas ça ?


j'ai aussi rajouté ma réponse à la question 4. pour la 5, je ne comprends rien du tout ...

[Noemi]

Pourquoi 3i puisque tu as x+2
c'est -2i - j
vérifie

[kalvy]

Ah oui, *quelle quiche!* j'étais tellement persuadée, que j'ai pas fait gaffe, mince ! -_-'

Sinon, pour la 4, ça va ce que j'ai fait ?

[Noemi]

Question 4.
Pour la résolution graphique:
Tu cherches les coordonnées des points d'intersection de la courbe et de la droite
f(x) < y si la représentation graphique de f est en dessous celle de la droite

Par le calcul :
Pour la résolution de l'inéquation, je propose :
S={x de R / x²+4x+3 inférieur ou égal (<) x+3}
S={x de R / x²+4x+3-x-3 < 0}
S={x de R / x²+3x<0}
S={x de R / x(x+3)<0} juste
Puis faire un tableau de signe ou appliquer une propriété
le résultat est x compris entre -3 et 0.

[Noemi]

Question 5
f(x) = x² - 4x + 3 = (x-2)²-1 à comparer avec la fonction étudiée précédemment
Il faut expliquer le tracé

Appliquer la même méthode avec les autres fonctions

[kalvy]

4) après avoir fait le tableau de signe, je retrouve bien l'intervalle : [-3;0]

5) je ne vois toujours pas ce que je dois faire comme explication ou calcul ...

[Noemi]

Question 5
Il faut comparer la fonction indiquée avec la fonction f

h(x) = x² - 4x + 3 = (x-2)²-1 or f(x) = (x+2)²-1
donc on effectue une translation de vecteur 4i comparaison de x-2 et x+2

[kalvy]

D'accord.
Et, quel est le lien, avec f(x) et les autres fonctions ? je ne vois pas du tout le rapport, encore moins quand on parle des valeurs absolues ...

[Noemi]

Tu dois écrire une relation entre les fonctions
k(x) = -x² - 4x = -f(x) + 3 puis tu traces la fonction en expliquant ta démarche.

[kalvy]

en fait, pour k(x), par exemple, je dois juste dire : k(x)=-f(x)+3 puis je trace la fonction ?

Et pour le 3eme alors, ça fait :
g(x) = |x²+4x+3| = |f(x)| = f(x) ou f(-x) ?

Mais la dernière, je la trouve bcp trop compliquée et je comprends pas du tout comment ça marche pr elle ...