Comparaison

par **fan de maths** » 03 Déc 2005, 22:17

Bonsoir,
voici une petite énigme qui m'a bien creusée les neuronnes:
Comparer rcd(2)+rcd(3) et ;) sans calculatrice.

J'ai trouvé mais ma méthode est un peu compliqué alors j'aimerais savoir comment vous raisonnez.

Bonne recherche.

par **Galt** » 03 Déc 2005, 23:33

Je ne comprends pas ce que signifie rcd(2)+rcd(3) ?
Désolé, mais j'ai besoin d'explications complémentaires

par **fan de maths** » 03 Déc 2005, 23:37

racine carrée de 2 + racine carrée de 3

par **Frangine** » 03 Déc 2005, 23:38

Et "n" qu'est-ce qu'il vient faire ici ?

Serait-ce un entier ? Quelle(s) condition(s) doit-il respecter ?

par **fan de maths** » 03 Déc 2005, 23:41

non en fait c'est pi

par **Galt** » 03 Déc 2005, 23:41

Alors, on doit pouvoir s'en sortir avec des encadrements de carrés :

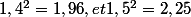
donc

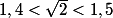
et de même

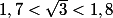
ce qui donne

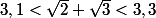
à moins que je n'aie pas bien compris l'énoncé ?

par **jawad** » 03 Déc 2005, 23:47

comapre les carrés
(rc2 + rc3)² = 5 + rc6

par **fan de maths** » 03 Déc 2005, 23:50

sauf que c'est (rc2 + rc3)² = 5 + 2rc6

par **jawad** » 03 Déc 2005, 23:58

oui c'est ça "très bien"

et après continue, c'est facile maintenant pour comparer "sans calculete"
si tu ne trouves pas fais signe...

par **jawad** » 04 Déc 2005, 00:02

en fait,
peux tu nous présenter "ta méthode un peu compliquée" pour voir ce que tu as trouvé

par **fan de maths** » 04 Déc 2005, 00:53

Alors avec plusieurs calculs à la main, on arrive à prouver que
(pi²-5)²<24
(pi²-5)²<(2sq6)²
comme pi²-5>0 et 2sq6>0
pi²-5<2sq6
pi²<5+2sq6
pi²<(sq2 + sq3)²
comme pi>0 et sq2 + sq3>0
pi
Mais c'est un peu compliqué et ça ne doit pas être la méthode la plus simple.

par **Galt** » 04 Déc 2005, 12:05

Je n'ai pas de méthode géométrique simple.
Avec la formule de Machin :

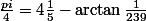
, puis en utilisant la formule

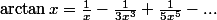
, j'obtiens

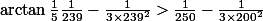
, ce qui donne finalement, après quelques calculs

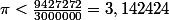
, ce qui permet de conclure

par **fan de maths** » 07 Déc 2005, 23:45

Bonsoir,
Est-ce que quelqu'un aurait une méthode réalisable par un élève de seconde ?
Merci

par **GaussFutur** » 31 Déc 2005, 20:51

bah c'est simple en fait :
on a :
(rc3 + rc2)²=5+2rc6
pi<5 implique que pi-5<0
et 5+2rc6-5=2rc6
et 2rc6>0
conclusion :
pi-5<0 2rc6>0 implique que pi-5<2rc6
pi<5+2rc6
pi<(rc3+rc2)²

euh... non j'vois pas pour la seconde... après j'ai des calculs trop lours !

Comparaison

comparaison

carré

Qui est en ligne