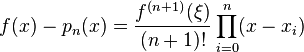 le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!
le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!Erreur interpolation lagrange
10 messages
- Page 1 sur 1
Erreur interpolation lagrange
Bonjour à tous, je viens de terminer la mise en place de mon tipe, seulement , n'ayant pu improviser sur l'erreur d'interpolation,le seul fruit de mes recherches est une expression créée à l'aide de la formule de taylor young, la voici 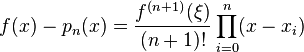 le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!
le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!
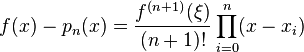 le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!
le seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!bilel59 a écrit:Bonjour à tous, je viens de terminer la mise en place de mon tipe, seulement , n'ayant pu improviser sur l'erreur d'interpolation,le seul fruit de mes recherches est une expression créée à l'aide de la formule de taylor young, la voicile seul huc est que cela fait longtemps que j'essaye de la décrypter en vain, puisse une âme charitable m'aider à comprendre , merci à vous!
J'ai une démonstration de cette formule dans mon cours d'analyse numérique :
http://clement-boulonne.123.fr/cours/m206.pdf (voir partie 2 : Analyse numérique)
Hello 
Une interprétation je ne sais pas trop, mais en tout cas une preuve est possible.
Alors on prend f une fonction n+1 fois dérivable, p un polynôme interpolant f aux points x_i et c [a;b]\{x0,x1,...,xn}
On pose-p(c)}{\Pi(c)}) et on considère
et on considère
Psi(x) = f(x) - p(x) - A. (x)
(x)
avec (x) = (x-x1)(x-x2)...(x-xn)
(x) = (x-x1)(x-x2)...(x-xn)
Vérifie que Psi s'annule n+2 fois.
Applique Rolle successivement (n+1) fois
Tu as que Psi(n+1) s'annule une fois.
Et tu peux conclure logiquement
Une interprétation je ne sais pas trop, mais en tout cas une preuve est possible.
Alors on prend f une fonction n+1 fois dérivable, p un polynôme interpolant f aux points x_i et c [a;b]\{x0,x1,...,xn}
On pose
Psi(x) = f(x) - p(x) - A.
avec
Vérifie que Psi s'annule n+2 fois.
Applique Rolle successivement (n+1) fois
Tu as que Psi(n+1) s'annule une fois.
Et tu peux conclure logiquement
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
