Bonjour, si quelqu'un peut m'aider à résoudre ce problème...
Un particulier à souscrit le 1er mars un crédit d'un montant de 35000 euros
Le remboursement s'effectue en 36 mensualités constantes de fin de période.
Le montant de chaque mensualité est de 1128,70 euros.
On désigne par t le taux d'interêt mensuel correspondant au coût réel de ce crédit, déterminé selon le principe des interêts composés.
1- exprimer, en fonction de t, le capital emprunté.
2- On précise que t est compris entre 0,5/100 et 1/100.
a.Donner une équation permettant de calculer t.
b. a l'aide de la calculette, calculer t à 10-4 prés par défaut.
c. calculer le taux actuariel i de ce crédit. On rapelle que i est le taux annuel équivalent au taux mensuel t.
Prob de maths financières, je cale !!!
8 messages
- Page 1 sur 1
par mathelot » 03 Mai 2008, 09:23
bjr,
je connais deux types d'emprunts, il y en a sûrement d'autre:
l'emprunt immobilier:
on emprunte un capital
, à taux mensuel t.
A la 1ère écheance, le montant
comporte un remboursement
d'intéret
et un remboursement de capital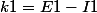 
.
On décrémente le capital restant dû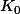
de 
et on recommence. ça donne l'échéancier de l'emprunt.
Il est possible que cet algorithme donne une formule explicite
liant le montant d'échéance, la durée du prêt et le capital emprunté.
à retrouver par un raisonnement par récurrence sur l'indice i de l'échéance.
l'emprunt inter-bancaire:
une banque emprunte un capital K0 sur le marché:
Les échéances comportent uniquement des paiements d'intérets.
La capital est lui, remboursé à la fin (in fine).
Pour un ordre d'idée:
un taux annuel de 12% donne un taux mensuel de l'ordre de 1%.
Un taux mensuel (à composition d'intérets mensuels) équivaut à un taux
actuariel annuel par la formule
^{12}=1+\frac{T_A}{100})
dans cette formule si T_A=12%, t est de l'ordre de 1%.
pour avoir des taux de même ordre, on compare en fait
et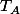 
.
je connais deux types d'emprunts, il y en a sûrement d'autre:
l'emprunt immobilier:
on emprunte un capital
A la 1ère écheance, le montant
d'intéret
On décrémente le capital restant dû
Il est possible que cet algorithme donne une formule explicite
liant le montant d'échéance, la durée du prêt et le capital emprunté.
à retrouver par un raisonnement par récurrence sur l'indice i de l'échéance.
l'emprunt inter-bancaire:
une banque emprunte un capital K0 sur le marché:
Les échéances comportent uniquement des paiements d'intérets.
La capital est lui, remboursé à la fin (in fine).
Pour un ordre d'idée:
un taux annuel de 12% donne un taux mensuel de l'ordre de 1%.
Un taux mensuel (à composition d'intérets mensuels) équivaut à un taux
actuariel annuel par la formule
dans cette formule si T_A=12%, t est de l'ordre de 1%.
pour avoir des taux de même ordre, on compare en fait
re
par wind65 » 03 Mai 2008, 09:36
:hein: :hein: Merci pour les infos
Plus simplement, y a t-il une formule pour calculer les intérêts mensuel t (sur le principe des intérêts composés) à partir de ce qu'on connait c'est à dire, :hein: du capital emprunté, des mensualités et du nombre de mensualités ?
Plus simplement, y a t-il une formule pour calculer les intérêts mensuel t (sur le principe des intérêts composés) à partir de ce qu'on connait c'est à dire, :hein: du capital emprunté, des mensualités et du nombre de mensualités ?
par mathelot » 03 Mai 2008, 09:52
bon, j'avais fait une erreur, relis mon post :hum:
on trouve la récurrence
 - E)
où
est le capital restant dû.
d'où une progression arithmético-géométrique.
Tu calcule la formule explicite de
puis le taux t en prenant
et 
Tchao,
on trouve la récurrence
où
d'où une progression arithmético-géométrique.
Tu calcule la formule explicite de
puis le taux t en prenant
Tchao,
par Quidam » 03 Mai 2008, 12:38
wind65 a écrit:Bonjour, si quelqu'un peut m'aider à résoudre ce problème...
Un particulier à souscrit le 1er mars un crédit d'un montant de 35000 euros
Le remboursement s'effectue en 36 mensualités constantes de fin de période.
Le montant de chaque mensualité est de 1128,70 euros.
On désigne par t le taux d'interêt mensuel correspondant au coût réel de ce crédit, déterminé selon le principe des interêts composés.
1- exprimer, en fonction de t, le capital emprunté.
2- On précise que t est compris entre 0,5/100 et 1/100.
a.Donner une équation permettant de calculer t.
b. a l'aide de la calculette, calculer t à 10-4 prés par défaut.
c. calculer le taux actuariel i de ce crédit. On rapelle que i est le taux annuel équivalent au taux mensuel t.
Si C est le capital emprunté, t le taux d'intérêt mensuel, n le nombre de mensualités, R la valeur des mensualités constantes, la relation qui lie ces quatre quantités est :
On peut ainsi exprimer directement R en fonction des trois autres, C en fonction des trois autres et m en fonction des trois autres. Par contre cela équivaut à une équation du m-ième degré en t. Connaissant C, m et R, il faut donc résoudre une équation du m-ième degré pour trouver t ! Impossible directement si m>4 !
En transformant la formule on obtient :
On peut trouver t par approximation successives. En donnant une valeur approximative pour
Et la suite
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :