Calcul d'une limite

par **quaresma** » 09 Avr 2008, 19:50

Bonjour à tous,
j'ai un exercice à faire sur les limites, mais je ne comprend strictement rien... :cry:

Dans l'énoncé, il donne une fonction:

La question est la suivante :
Calculer la limite de t en + l'infini. Interpreter ce résultat.

Je ne sais pas du tout comment mis prendre. Pourriez-vous me montrer les étapes à effectuer pour calculer la limite ?

Merci encore. :mur:

par **trust** » 09 Avr 2008, 19:58

par **quaresma** » 09 Avr 2008, 20:06

'lut trust,
le résultat seul ne m'interesse pas vraiment.
Ce que je veux comprendre c'est la manière dont tu trouves ce résultat... :hein:

par **nonam** » 09 Avr 2008, 20:18

Il faut connaitre les limites classiques...
ln(x) est négligeable en

devant

, du coup la limite de

est nulle. De même pour

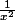
. Et donc tu peux conclure par linéarité de lim.

par **quaresma** » 09 Avr 2008, 20:24

Il faut connaitre les limites classiques...
ln(x) est négligeable en devant

Qu'entends-tu par "négligeable" ? :id:

Et le

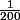
que vaut-il ?

par **quaresma** » 10 Avr 2008, 09:06

un pti up pour une ptite aide :briques:

par **cesar** » 10 Avr 2008, 09:42

quaresma a écrit:
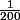
Et le que vaut-il ?

elle est bien bonne !!! c'est la premiere fois que je vois ce coup là... :ptdr:

ps : que veux tu que fasse une constante, à part rester constante...

par **quaresma** » 10 Avr 2008, 09:55

nonam a écrit:Il faut connaitre les limites classiques...
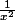
ln(x) est négligeable en devant , du coup la limite de est nulle. De même pour . Et donc tu peux conclure par linéarité de lim.

Qu'entends-tu par "négligeable" ? :id:

par **jver** » 10 Avr 2008, 10:04

cesar a écrit:elle est bien bonne !!! c'est la premiere fois que je vois ce coup là... :ptdr:

ps : que veux tu que fasse une constante, à part rester constante...

Elle n'est pas mal! mais il y a aussi la technique de "variation de constante"!!!

par **quaresma** » 10 Avr 2008, 10:24

nonam a écrit:Il faut connaitre les limites classiques...
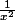
ln(x) est négligeable en devant , du coup la limite de est nulle. De même pour . Et donc tu peux conclure par linéarité de lim.

Qu'entends-tu par "négligeable" ? :id:

par **nonam** » 10 Avr 2008, 12:03

écris "négligeable" sur google et tu auras directement la définition mathématique du terme (sur wikipédia)...
Mais même si tu n'as pas vu les notions d'équivalents, négligeabilité etc... la limite de

, c'est du niveau lycée. Ils appellent ca "croissance comparée" je crois.

par **quaresma** » 10 Avr 2008, 13:54

Ok merci je vais essayer de comprendre...

Calcul d'une limite

Calcul d'une limite

Qui est en ligne