Bonjour, j'ai des difficultés pour quelques questions. Ce serait sympa si vous pouviez jeter un oeil pour éventuellement m'aider. Merci.
c)Montrer que pour tout entier naturel non nul n, on a: n! >= e(n/e)^n.
Pour qu'on ait cela, il faut que n! - e(n/e)^n >= 0.
Alors on peut introduire la fonction f(x) = n! - e(n/e)^n
Et ensuite, comment montrer que dans cette soustraction, c'est n! qui est plus grand? (enfin c'est comme cela que je le vois )
ex8:
On considère la suite u définie par u0 réel compris strictement entre 0 et 1 et la relation: Vn E N, u_n+1 = (1-rac(1-un)) / 3.
a) Montrer que pour tout entier naturel n le terme un est bien défini et 0 < u_n < 1.
Ok
b) Montrer que pour tout entier naturel n, on a:
u_n+1 =< (1 / 3)(u_n).
Votre aide est la bienvenue, je vous concède que cette question n'est pas d'un extrême difficulté, et pourtant je demande de l'aide.
Voila. merci.
Petits pbs
5 messages
- Page 1 sur 1
Bonjour,
Pour le 2), le plus simple est de calculer et montrer que cette différece est positive.
et montrer que cette différece est positive.
Indication: si A appartient à [0 ; 1] alors
Ca nous donne donc: un/3 - un+1 > 0
(un - 1 - rac.( 1 - un)) / 3 > 0
La fonction n'admet que des valeurs positives donc c'est positif.
Mais je sais pas quoi dire d'autre :hum:
Pour le premier exercice:j'aurais tendance à passer au ln, mais tu devrais nous fournir les question a) et b)
a) montrer que pour tout réel x positif ou nul, on a: ln(1+x) ==1 par: un = 1/n! (n/e)^n. Montrer que (un)n>=1 est monotone. (au passage je n'ai pas réussi cette question mais je me disais que c'était trop facile pour demander de l'aide)
Bon courage
Merci bien
Pour le 2), le plus simple est de calculer
Indication: si A appartient à [0 ; 1] alors
Ca nous donne donc: un/3 - un+1 > 0
(un - 1 - rac.( 1 - un)) / 3 > 0
La fonction n'admet que des valeurs positives donc c'est positif.
Mais je sais pas quoi dire d'autre :hum:
Pour le premier exercice:j'aurais tendance à passer au ln, mais tu devrais nous fournir les question a) et b)
a) montrer que pour tout réel x positif ou nul, on a: ln(1+x) ==1 par: un = 1/n! (n/e)^n. Montrer que (un)n>=1 est monotone. (au passage je n'ai pas réussi cette question mais je me disais que c'était trop facile pour demander de l'aide)
Bon courage
Merci bien
Pour le 2) ton argument est incompréhensible : c'est positif car "La fonction n'admet que des valeurs positives " ????
De quelle fonction parles-tu ? de plus tu as fait une erreur de signe
tu as[u_n - 1 + \sqrt{1 - u_n}])
Utilise mon indication en posant
vérifie que A appartient bien à [0 ; 1], compare alors A et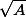 puis conclus sur le signe de
puis conclus sur le signe de 
pour le 1.
tout s'éclaire : pour démontrer que) est monotone, compare
est monotone, compare 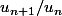 et 1 (c'est possible car tu as une suite dont tous les termes sont positifs)
et 1 (c'est possible car tu as une suite dont tous les termes sont positifs)
Montre que^n)
Grâce à la question a), prouve que < 0) tu pourras alors comparer
tu pourras alors comparer 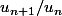 et 1 et conclure que la suite
et 1 et conclure que la suite ) est décroissante
est décroissante
Ensuite la question c) devient facile: si la suite est décroissante alors
est décroissante alors  , calcule
, calcule  , tu en déduiras que
, tu en déduiras que  et en multipliant par n! tu obtiendras l'inégalité cherchée.
et en multipliant par n! tu obtiendras l'inégalité cherchée.
De quelle fonction parles-tu ? de plus tu as fait une erreur de signe
tu as
Utilise mon indication en posant
vérifie que A appartient bien à [0 ; 1], compare alors A et
pour le 1.
tout s'éclaire : pour démontrer que
Montre que
Grâce à la question a), prouve que
Ensuite la question c) devient facile: si la suite
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
