bonjour tout le monde je suis nouveau , jevouq pose mon problème :
pour tout x non nul on pose u(x) =x² et v(x)=2/x
soit la fonction definie sur R par f(x):u(x)+v(x)
1) indiquer le sens de variations de u et de v sur chacun des intervalles ]-infini;0[ et ]0;+infini[.
2) Que peut on dire du sens de variation de f sur ]0;+infini[?
de f sur ]- infini;0[?
Voilà je suis bloqué si quequ un pouvait m'aider ce serait super .
Aidez moi. fonction
12 messages
- Page 1 sur 1
luigiciciretti a écrit:bonjour tout le monde je suis nouveau , jevouq pose mon problème :
pour tout x non nul on pose u(x) =x² et v(x)=2/x
soit la fonction definie sur R par f(x):u(x)+v(x)
1) indiquer le sens de variations de u et de v sur chacun des intervalles ]-infini;0[ et ]0;+infini[.
2) Que peut on dire du sens de variation de f sur ]0;+infini[?
de f sur ]- infini;0[?
Voilà je suis bloqué si quequ un pouvait m'aider ce serait super .
salut t bloqué ou?
luigiciciretti a écrit:Salut merci de repondre ben deja au niveau de x² = u(x) ça me bloque pareil pour v(x)=2/x après les deux questions je n sais absolument pas comment faire je uis bloqué totallemet si tu pouuvais m aider.
tu sais calculer une dérivée? etudier son signe? et en deduire un tableau de variation?
Bonjour
Tu dois savoir répondre à cette question : la réponse est dans ton cours !pour tout x non nul on pose u(x) =x² et v(x)=2/x ... 1) indiquer le sens de variations de u et de v sur chacun des intervalles ]-infini;0[ et ]0;+infini[.
Voilà je suis bloqué si quequ un pouvait m'aider ce serait super .
luigiciciretti a écrit:je suis en terminal mais j ai été beacoup absent l année dernière si je demande c est pas pour rien rené.
Un petit rappel te feras pas de mal alors:
(u^n)'=n*u'*u^(n-1)
(1/u)'=-u'/u²
donc on applique à ton pb
u(x)=x² donc u'(x)=2*x tu connais le signe de u'(x) sur R... donc t'en deduis ses variations.
v(x)=2/x donc v'(x)=-2/x² <0 donc v est décroissante...
C'est un problème qui pourrait être posé en seconde !
En effet, on apprend en seconde que la somme de deux fonctions croissantes est croissante, que la somme de deux fonctions décroissantes est décroissante. On apprend aussi que le produit d'une fonction croissante (resp. décroissante) par une constante positive est croissant (resp. décroissant)
Donc, en seconde, on pourrait répondre :
1) indiquer le sens de variations de u et de v sur chacun des intervalles ]-infini;0[ et ]0;+infini[.
La fonction u est décroissante sur l'intervalle et croissante sur l'intervalle
et croissante sur l'intervalle 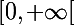
C'est le cours de seconde, ni plus, ni moins !
La fonction v est le produit de la fonction inverse (1/x) par la constante positive 2. On sait que la fonction inverse est décroissante sur l'intervalle et également décroissante sur l'intervalle
et également décroissante sur l'intervalle  . Par conséquent la fonction v est décroissante sur l'intervalle
. Par conséquent la fonction v est décroissante sur l'intervalle  et également décroissante sur l'intervalle
et également décroissante sur l'intervalle 
2) Que peut on dire du sens de variation de f sur ]0;+infini[?
de f sur ]- infini;0[? Toujours en seconde, on peut donc répondre que sur l'intervalle , les fonctions u et v étant toutes deux décroissantes, la fonction f, somme de deux fonctions décroissantes, est décroissante.
, les fonctions u et v étant toutes deux décroissantes, la fonction f, somme de deux fonctions décroissantes, est décroissante.
Et sur l'intervalle , la fonction u étant croissante et la fonction v décroissante, on ne peut pas conclure a priori sur la fonction f.
, la fonction u étant croissante et la fonction v décroissante, on ne peut pas conclure a priori sur la fonction f.
Par contre, en première, on apprend la dérivation, et on peut alors déterminer plus finement la croissance et la décroissance de f selon la valeur de la variable x. Mais, étant donné que la question est posée sur les deux intervalles et
et  , je pense que la réponse attendue est tout simplement que l'on ne peut pas conclure sans autres investigations !
, je pense que la réponse attendue est tout simplement que l'on ne peut pas conclure sans autres investigations !
En effet, on apprend en seconde que la somme de deux fonctions croissantes est croissante, que la somme de deux fonctions décroissantes est décroissante. On apprend aussi que le produit d'une fonction croissante (resp. décroissante) par une constante positive est croissant (resp. décroissant)
Donc, en seconde, on pourrait répondre :
1) indiquer le sens de variations de u et de v sur chacun des intervalles ]-infini;0[ et ]0;+infini[.
La fonction u est décroissante sur l'intervalle
C'est le cours de seconde, ni plus, ni moins !
La fonction v est le produit de la fonction inverse (1/x) par la constante positive 2. On sait que la fonction inverse est décroissante sur l'intervalle
2) Que peut on dire du sens de variation de f sur ]0;+infini[?
de f sur ]- infini;0[? Toujours en seconde, on peut donc répondre que sur l'intervalle
Et sur l'intervalle
Par contre, en première, on apprend la dérivation, et on peut alors déterminer plus finement la croissance et la décroissance de f selon la valeur de la variable x. Mais, étant donné que la question est posée sur les deux intervalles
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
