DM de math cgpe

[Margaux132]

bonjour, j'ai un dm de math pour lundi et j'ai quelques petites difficultés sur certains points:

1) démontrer que pour tout n>5, 3^n/n! < 1/2^n-7

2) démontrer qu'à partir d'un certain tang N, n!>3^n

3) demontrer que pour tout n>1, 3*5^2n-1+2^3n-2 est divisible par 17.

Merci d'avance
Margaux

[abcd22]

Bonjour,

bonjour, j'ai un dm de math pour lundi et j'ai quelques petites difficultés sur certains points:

1) démontrer que pour tout n>5, 3^n/n! 3^n

C'est équivalent à n!/3^n > 1 à partir d'un certain rang, quelle est la limite de n!/3^n ?

3) demontrer que pour tout n>1, 3*5^2n-1+2^3n-2 est divisible par 17.

Là aussi il faut mettre les parenthèses...

[Margaux132]

démontrer que pour tout n>5, 3^n/n! < 1/2^(n-7)


3) demontrer que pour tout n>1, 3*5^(2n-1)+2^(3n-2) est divisible par 17

[abcd22]

Pour le 3 on peut remarquer que 17 = 3×5 + 2 et écrire

ensuite utiliser les propriétés des congruences, des puissances...

[abcd22]

Pour le 1 c'est équivalent à montrer :
* n! : n facteurs 1, 2, ... n, donc quand n est grand il y a de grands facteurs,
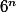* : n facteurs aussi mais tous égaux à 6 cette fois, donc intuitivement on sent bien que le terme de droite (dans l'inégalité que j'ai écrite) sera plus grand que celui de gauche pour n assez grand, il faut juste le rédiger rigoureusement, le 2^7 sert pour les valeurs proches de 6 pour lesquelles .