Blocage sur une inégalité...

[Erana]

La rentrée est dure pour moi en fac de maths-éco!

Je suis en train de me prendre la tête sur l'inégalité suivante:

2^n supérieur ou égal à (n+1)²

Désolé mais je ne sais pas comment on fait les puissances sur cet ordi :S

En espérant que vous pourrez m'aider...

Charles

[nuage]

Salut,
.
Or on démontre que qui est négligeable devant .
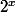
Tout ceci dans un voisinage de

[Erana]

Le problème est que je dois trouver à partir de quel rang l'inégalité est vraie en fait...

[Erana]

J'ai toujours besoin d'aide pour savoir à partir de quel rang l'inégalité est vraie...

[fahr451]

n = 0 ok

on suppose au rang n

au rang n+1

on veut 2^n >= ln (n+2)

on a 2^(n-1) >= ln(n+1)

il suffit d'avoir (n+1)^2 >=n+2 ce qui est vrai

[Erana]

Erm je sais, je suis un boulet, mais le logarithme que j'avais mis dans l'énoncé n'avait rien à y faire, j'ai mélangé brouillon et énoncé :S

La vraie inégalité est dans le cadre désormais!

[yos]

J'ai toujours besoin d'aide pour savoir à partir de quel rang l'inégalité est vraie...

Essaie, n=0,1,2,3... c'est vite règlé.

[Erana]

C'est la solution de facilité...

Mais je voulais RESOUDRE cette inégalité sans y aller à tatons!

Toujours personne pour la résoudre mathématiquement alors?

[fahr451]

C'est la solution de facilité...

Mais je voulais RESOUDRE cette inégalité sans y aller à tatons!

Toujours personne pour la résoudre mathématiquement alors?

feignants et nuls sur ce site !

[yos]

C'est la solution de facilité...

Mais je voulais RESOUDRE cette inégalité sans y aller à tatons!

Toujours personne pour la résoudre mathématiquement alors?

Ne dis pas n'importe quoi. Des essais montrent que l'inégalité est vraie pour n=6 et tu engages la récurrence à partir de là : c'est ça faire des mathématiques.