Bonjour,
J'aimerai bien de trouver la suite decrite dans l'énonce ci-dessous sous forme mathématique, une somme. :help:
merci d'avance pour tout vos réponses :++:
-------
On s'intéresse aux nombres entiers de n chiffres ayant la propriété suivante: en partant des chiffres composant ces nombres, on compose une suite en calculant la somme des n derniers nombres de la suite pour déterminer le suivant. La suite fournit à un moment le nombre de départ.
Exemple:
K=197 (les chiffres de départ sont 1, 9 et 7).
1,9,7,17(=1+9+7),33(=9+7+17),57(=7+17+33),107(=17+33+57),197(=33+57+107)
Nous concluons donc que 197 possède la propriété énoncée plus haut puisque ce nombre se retrouve lui-même dans la suite.
C quelle suite ça????
5 messages
- Page 1 sur 1
problème intéressant, je fais remonter le fil...
formalisons, pour débroussailler:
je propose déja le cas n=2:
Soit où
où 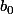 et
et  sont deux chiffres.
sont deux chiffres.
Soit la suite) définie par la récurrence:
définie par la récurrence:

et la condition initiale:


On s'arrête quand .
.
à priori, on voit apparaitre le nombre d'or dans l'équation:
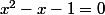 et la suite de Fibonacci.
et la suite de Fibonacci.
Cordialement,
formalisons, pour débroussailler:
je propose déja le cas n=2:
Soit
Soit la suite
et la condition initiale:
On s'arrête quand
à priori, on voit apparaitre le nombre d'or dans l'équation:
Cordialement,
Salut,
en tous cas il semble qu'il n'y ai pas beaucoup de tels nombres :
Voici la liste de ceux qui sont inférieurs à 10000 :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909.
A part ceux à un chiffre j'ai fait une recherche systématique avec un petit programme ad hoc.
en tous cas il semble qu'il n'y ai pas beaucoup de tels nombres :
Voici la liste de ceux qui sont inférieurs à 10000 :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909.
A part ceux à un chiffre j'ai fait une recherche systématique avec un petit programme ad hoc.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
