Bonjour,
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 18:43
par cassandra28 » 04 Sep 2007, 18:43
Soit la suite Un, définie par Uo=2. U(n+1)= 2Un-3 (n entier naturel)
calculer U1, U2, U3, U4 et conjecturer Un,
l'exercice est en soi assez simple mais je ne parviens pas à conjecturer, merci de bien vouloir m'aider :)
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 18:54
par Clembou » 04 Sep 2007, 18:54
cassandra28 a écrit:Soit la suite Un, définie par Uo=2. U(n+1)= 2Un-3 (n entier naturel)
calculer U1, U2, U3, U4 et conjecturer Un,
l'exercice est en soi assez simple mais je ne parviens pas à conjecturer, merci de bien vouloir m'aider

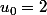
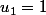
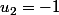
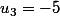
...
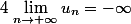
En fait, c'est une suite reccurente. Soit
 = 2x-3)
alors :
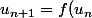)
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 18:56
par cassandra28 » 04 Sep 2007, 18:56
je suis désolée je ne comprends pas en quoi cela me permet de trouver l'expression de Un...
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 18:56
par cassandra28 » 04 Sep 2007, 18:56
pardon, je navais pas eu le fin du message affichée
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 18:58
par cassandra28 » 04 Sep 2007, 18:58
j'avais remarqué en effet qu'il s'agissait d'une suite récurrente, mais mon problème me semble plutot venir de la logique, puisque je ne parviens pas à trouver l'expression de Un...
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 19:01
par Clembou » 04 Sep 2007, 19:01
cassandra28 a écrit:je suis désolée je ne comprends pas en quoi cela me permet de trouver l'expression de Un...
Ah ! Tu veux une expression sous forme :
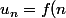)
On a alors :
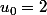
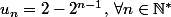
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 19:09
par cassandra28 » 04 Sep 2007, 19:09
pourtant, U2= -1, or si Un=2-2^(n-1), U2= 2-2^(2-1)=0
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 19:18
par fahr451 » 04 Sep 2007, 19:18
bonsoir
regarde sur google suite arithmético géométrique
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2007, 19:19
par Clembou » 04 Sep 2007, 19:19
cassandra28 a écrit:pourtant, U2= -1, or si Un=2-2^(n-1), U2= 2-2^(2-1)=0
Ah oui très juste ! J'ai voulu faire les différences entre les u_n...
En fait, c'est :
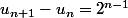
Mais après je ne sais pas !
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 19:29
par cassandra28 » 04 Sep 2007, 19:29
merci pr les sites mais je n'y arrive vraiment pas, peut etre qu'une explication me serait plus utile...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 19:30
par fahr451 » 04 Sep 2007, 19:30
on a
u(n+1) = 2u(n) - 3 (1)
choisis un réel L qui vérifie
L = 2L - 3 (2)
fais (1) - (2)
pose v(n) = u(n) -L et constate que v est géométrique
déduis en v(n), calcule L et déduis en u(n)
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 04 Sep 2007, 20:35
par cassandra28 » 04 Sep 2007, 20:35
je suis désolée, je dois etre fatiguée, mais je ne comprends strictement rien...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 22:34
par fahr451 » 04 Sep 2007, 22:34
ah
alors
on a u(n+1) = 2u(n) - 3 (1)
(normalement là ça va c 'est ton énoncé)
on a aussi
3 = 2x3 - 3 (2)
(normalement ça va toujours)
(1)- (2) donne
u(n+1) - 3 = 2 [ u(n) -3]
donc en posant v(n) = u(n) - 3 on a
v(n+1) = 2 v(n)
(je suis confiant ça devrait aller)
donc v(n) = 2 ^n v(0)
(suite géométrique )
puis u(n) = 2^n ( 2-3) +3 = 3 - 2^n
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 05 Sep 2007, 19:16
par cassandra28 » 05 Sep 2007, 19:16
merci, je pense avoir enfin compris, seulement vu que je commence a peine ce chapitre sur les suites et que je ne savais pas que l'on pouvait poser une valeur particulière telle que L, je ne pouvais pas comprendre...
Encore une fois merci beaucoup :)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Sep 2007, 19:36
par fahr451 » 05 Sep 2007, 19:36
je t'ai donné la méthode générale pour exprimer un en fonction de n
on n'attendait pas ça de toi je pense mais plutôt de calculer les premiers termes pour
"trouver empiriquement" l'expression et ensuite le démontrer par récurrence
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 05 Sep 2007, 21:12
par cassandra28 » 05 Sep 2007, 21:12
c'est ce que je pensais egalement, seulement, comment je peux faire dans ce cas avec cet enoncé:
Uo=3
U(n+1)= -Un+4
je calcule U1=1 U2=3 U3=1 U4=3...
On me demande de conjecturer, puis de determiner Un en fonction de n...
je ne vois qu'une manière littérale d'exprimer cette suite, en dissociant n pair de n impair
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Sep 2007, 22:04
par fahr451 » 05 Sep 2007, 22:04
n'arrives tu pas à refaire ce que j'ai déjà fait ?
avec L bien choisi ...
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 05 Sep 2007, 22:15
par cassandra28 » 05 Sep 2007, 22:15
L=2
U(n+1)-2=(-Un+4)-2 ...mais après, comment je definis ma suite auxiliaire Vn?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Sep 2007, 22:17
par fahr451 » 05 Sep 2007, 22:17
vn = un -2
-
cassandra28
- Membre Naturel
- Messages: 30
- Enregistré le: 02 Sep 2007, 10:51
-
 par cassandra28 » 05 Sep 2007, 22:42
par cassandra28 » 05 Sep 2007, 22:42
c'est ce que j'avais trouvé mais jme suis pas fait confiance et j'ai pas poursuivi ma démo. Je viens de la terminer, merci beaucoup!! Bonne soirée!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
