Bonjour

[irazboubi]

Hier j'ai demandé de l'aide sur un exercice qui était le suivant

soit ABCD un parallélogramme.
1)soit le point E vérifiant : 3AE+4CE+AEB=3(DE+DC)
2)exprimer EA en fonction de ED
3)Soit F lintersection de (AB) avec (EC). Exprimer EF en fonction de EC
4)Exprimer BE en fonction de AB et AC, puis CE en fonction de AB et de AC
5)placer le point G tel que CG = -1/4AB+1/3AC
6)Démontrer que les points E,C et G sont alignés

on m'a effecctivement aidé mais je ne comprend pas les expliquations de la question 2 qui sont : 3AE+4CE+7EB=3(DE+DC)
3AE+4(CE+EB)+3EA+3AB=3DE+3DC
pouvez vous m'expliquer comment on passe de 3AE+4CE+7EB=3(DE+DC) à 3AE+4(CE+EB)+3EA+3AB

à la question 1 je trouve que AE=7/3CB+2AD est ce juste? Car la question 6 m'en prétend le contraire car je trouve que E,C et G ne sont pas ailgnés par construction

merci d'avance

[armor92]

Bonjour irazboubi,

Pour la question 2)
On part de la relation :

(on remplace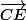 par )

(on remplace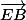 par )

(On fait passer du membre de droite vers le membre de gauche)

(On remarque car ABCD parallélogramme)




3) On utilise le théorème de thalès dans le triangle EDC.
EA / ED = EF / EC = 1/4
Donc EF = EC /4
De l'égalité sur les distances, on déduit l'égalité sur les vecteurs.

[armor92]

4) On démontre d'abord que .
On a démontré dans le 2) que




On a démontré que :




( on sait que )






( on sait que )

[armor92]

5)
On place le point G sur un graphique à partir du point C

6) On doit démontrer que les vecteurs et sont colinéaires.


On a démontré dans le 4) que :


C'est curieux mais je ne trouve pas qu'ils sont colinéaires.

Il doit y avoir une erreur quelque part dans ton énoncé

[armor92]

7)exprimer BG en fonction de CA et de BD

(1)

Le problême est d'exprimer et en fonction des vecteurs et

Pour cela on écrit le systeme :
(2)
(3)

(2) + (3) donne :
(3) - (2) donne :

On a donc :

et


On en revient à , la relation (1) s'écrit :
=
=

[armor92]

8)soit O le centre du parallélogramme ABCD.

exprimer OE en fonction de AC et de BD

(1)

O est le centre du parallélogramme, donc O est le milieu du segement [AC], cela se traduit par la relation sur les vecteurs :
(2)

D'autre part, on a démontré dans le 4) que : (3)

Hors on a montré dans le 7) que : (4)

De (3) et (4) on déduit que :


La relation (1) devient :

[armor92]

9) Soit T le point tel que DT = 1/3DA

soit H l'intersection de (AB) avec la parallèle à (BD) passant par T

a)exprimer AH en fonction de AB

On a AT = 2/3 AD

On peut appliquer le théoréme de THALES dans le triangle ABD.
AT / AH = AD / AB

AH = AT * AB / AD
AH = 2/3 AB
De cette relation découle l'égalité sur les vecteurs :


b)exprimer FH en fonction de AB
On peut démontrer en utilisant le théorème de THALES que :