Un problème de statistique dans un livre de SF

[benoith]

Bonjour.
Je suis Benoit, soignant de 50 ans.

Je suis en train d'écrire mon premier livre de sf.
C'est de la hard sf. Tout ce que j'écris doit être en accord avec la réalité.

Et je me retrouve dans face à une énigme que je ne sais pas résoudre.

J'ai besoin de l'aide d'un mathématicien.

Le problème des mille urnes

Mille urnes sont disposées devant vous.
L'urne numéro contient k billes blanches et 1000 − k billes colorées.

Vous choisissez une urne au hasard, puis tirez des billes sans remise.
Les premières sont toutes blanches.

Question: Combien de billes blanches consécutives faut-il observer pour que l'urne mille — celle qui ne contient que des blanches — devienne l'hypothèse la plus probable ?

Merci

[phyelec]

Bonjour,

L'urne numéro contient k billes blanches et 1000 − k billes colorées.

quelle le numéro de cette urne? est k?
si j'ai bien compris : les Mille urnes sont numérotés et on en choisit une au hasard (donc on a les yeux bandés?)et vous voulez connaître au bout x tirage n billes la probabilité d'avoir choisit l'urne 1000?
est-ce que chaque urne contient le même nombre de billes?

[GaBuZoMeu]

Bonjour,

Si on a tiré sans remise boules blanches à la suite, la probabilité d'avoir tiré dans l'urne n° est , sauf erreur (remarquer que 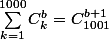). Si on prend 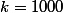, cette probabilité est .
Remarque : avant tout tirage, toutes les urnes ont la même probabilité d'avoir été choisies. Dès qu'on a tiré une boule blanche, c'est l'urne n°1000 qui a le plus de probabilité d'avoir été choisie. Mais si on interprète la question comme "à partir de combien de boules blanches tirées a-t-on plus d'une chance sur deux d'avoir tiré l'urne n°1000 ?", la réponse est 500.