Exercice système matriciel

[Joula]

Bonjour à tous,
Je rencontre un problème avec un exercice sur les matrices:
On me demande dans l'exercice si il existe un/plusieurs triplets avec tels que :
avec et si oui, le/lesquels
après résolution d'un système je trouve un triplet solution mais je n'arrive pas à déterminer si ce dernier est unique
merci d'avance !

[hdci]

Bonjour,

Vous trouvez un triplet dépendant de z (je n'ai pas vérifié les calculs).

Essayez avec z=0 : est-ce que cela marche ?
essayez avec z=1 : est-ce que cela marche ?

De façon générale, si vous trouvez un triplet qui s'exprime en fonction de z, cela fait autant de triplets possibles que de valeurs possibles pour z. Combien z peut-il prendre de valeurs... ?

PS. Puisqu'on cherche des solutions x, y, z dans IR, cela fait qu'il y a soit aucune, soit une unique, soit une infinité de solutions.

[Joula]

Merci pour votre réponse, si on prend z=0 l'équation reste vraie mais d'après mon énoncé (qui se base sur des probabilités), on a d'abord posé x+y+z=1 à priori donc je pense qu'il existe une unique solution car si on prend z=1/5 on à bien x+y+z=1

[hdci]

d'après mon énoncé (qui se base sur des probabilités), on a d'abord posé x+y+z=1 à priori donc je pense qu'il existe une unique solution car si on prend z=1/5 on à bien x+y+z=1

Ah oui, si vous ne donnez pas tout l'énoncé avant...

Car sans cette condition, il y a bien une infinité de solutions et le triplet que vous trouvez est correct. En ajoutant la condition x+y+z=1, alors z=1/5 est la seule valeur possible pour z, puisque

(11/4)z+(5/4)z+z=1 équivaut à 20z=4 donc z=20/4=1/5.

[Joula]

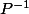
Oui veuillez m'excuser, l'énoncer ne l'explicitait pas clairement ce n'est qu'en relisant que j'ai compris... Je rencontre un autre soucis sur cet exercice, on pose une matrice P telle que Montrer que P est inversible et calculer, en classe nous avons appris la méthode pour montrer qu'une matrice est inversible uniquement sur une matrice 2x2, comment procède-t-on pour une matrice 3x3 ? Je saurais calculer l'inverse de P à l'aide de la méthode de Gauss mais je ne sais pas comment d'abord montrer qu'elle est inversible. Encore une fois merci d'avance.

[Vassillia]

Bonjour, tu n'as jamais entendu parler de déterminant ?
Car s'il est non nul, cela montre que la matrice est inversible.

[Joula]

Bonjour, non justement, j'ai regardé plusieurs fois mon cours et la notion de déterminant n'y figure pas...

[Vassillia]

Tant pis, on va faire les 2 en même temps alors, tu peux commencer par utiliser la méthode du pivot de Gauss, lorsque tu as une matrice triangulaire supérieure, si tous ses pivot sont différents de 0 alors la matrice est inversible. Tu peux ensuite finir la méthode

[Joula]

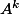
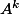
Bonjour, j'ai déterminé la matrice inverse de P sans accroc, je rencontre un dernier soucis avec l'explicitation de la matrice je pense qu'il faut que je trouve une expression de par le calcul que je confirmerais par récurrence pensez vous que c'est la bonne méthode ?