On peut voir cela de façon très pratique : au marché, il y a des paniers qui comportent 4 pommes et 5 poires.
Si j'achète 10 paniers, j'ai bien 10 fois (4 pommes+5 poires) ce qui fait 40 pommes et 50 poires.
Complètement différent de 10 fois 4 pommes, plus 5 poires.
C'est pour cela que la multiplication, quand elle multiplie "un tout", oblige à mettre des parenthèses.
Supposons maintenant que les pommes soient en fait découpées en petits cubes, et les poires en petites pyramides. Chaque pomme est découpée en 15 cubes et chaque poire en 20 pyramides.
Avoir acheté 10 paniers, cela revient à faire 10 fois (15 fois 4 cubes, plus 20 fois 5 pyramides).
Le facteur 10 est là encore devant une parenthèse, car le calcul du nombre de cubes et de pyramides, dans un panier, se fait à l'intérieur du panier. Le 10 ne vient multiplier cela qu'après : j'ai bien finalement 10 fois (60 cubes plus 100 pyramides).
enfin, si j'achète 10 paniers, plus 4 steak (qui n'ont rien à voir avec les paniers), les 4 steacks sont bien ajoutés à part donc hors des parenthèses, et pas du tout multipliés par 10
C'est le même principe avec
^2-5)
: le facteur 4 multiplie l'expression
^2)
, car une règle de priorité dit qu'on effectue d'abord le calcul des puissances avant tout autre calcul.
Ici on veut que ce soit tout
)
qui soit élevé au carré : si j'écris

, par priorité seul le 2 est élevé au carré et cela donne
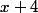
, alors qu'en fait je veux faire
(x+2))
.
Par contre, le 4 est hors des parenthèses donc n'est pas élevé au carré ; mais il multiplie l'ensemble de
^2)
, ce qui fait qu'après avoir calculé
^2=x^2+4x+4)
quand je multiplie par 4 je multiplie bien toute cette expression et pas seulement le premier terme. D'où les parenthèses
)
Le -5 étant hors des parenthèses, c'est comme pour les steaks du marché, c'est traité "à part" donc hors des parenthèses.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.

