[1ère]Exercice dérivation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 17:06
par tonypeter » 06 Déc 2006, 17:06
Bonjour à tous,
J'ai un exo pour demain que je n'arrive absolument pas à faire (je suis bloqué à la question 1):
J'ai passé 1h à cherche sans résultats...
Voici la question:
1)a)H est un réel non nul . Justifier les égalités suivantes:
}{h} \right)=\left( \frac{2(\sin^2(h/2))}{h} \right)=\left( \frac{\sin(h/2)}{h/2} \right)*\sin(h/2))
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 17:12
par theluckyluke » 06 Déc 2006, 17:12
tonypeter a écrit:Bonjour à tous,
J'ai un exo pour demain que je n'arrive absolument pas à faire (je suis bloqué à la question 1):
J'ai passé 1h à cherche sans résultats...
Voici la question:
1)a)H est un réel non nul . Justifier les égalités suivantes:
EDIT: attendez quelque secondes...

yup ça marche!
(tu peux mettre un 3$ juste apres le [TEX] pour afficher plus grand (3$, 4$, 5$, etc. mais bon sans abuser)
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 17:13
par tonypeter » 06 Déc 2006, 17:13
Ok merci :)
Sinon t'as la réponse au problème ? lol j'abuse de ta bonté :we:
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 17:15
par theluckyluke » 06 Déc 2006, 17:15
tonypeter a écrit:Ok merci

Sinon t'as la réponse au problème ? lol j'abuse de ta bonté :we:
carré : x^2 et plus généralement x^{n+1}
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 17:21
par tonypeter » 06 Déc 2006, 17:21
Ca marche!
Petites précisions pour l'exo :
=\sin(a)\times\cos(b)+\sin(b)\times\cos(a))
=\cos(a)\times\cos(b)-\sin(a)\times\sin(b))
=1-2\sin^2(a))
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 17:22
par theluckyluke » 06 Déc 2006, 17:22
tonypeter a écrit:Ca marche!
Petites précisions pour l'exo :
=\sin(a)*\cos(b)+\sin(b)*\cos(a))
=\cos(a)*\cos(b)-\sin(a)*\sin(b))
=1-2\sin^2(a))
bon je t'aide, juste un truc :
le "fois", c'est \times
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 17:29
par theluckyluke » 06 Déc 2006, 17:29
bon deja, pour passer de la deuxieme à la troisième partie
 = [sin(\frac{h}{2})]^2 = sin(\frac{h}{2}) \times sin(\frac{h}{2}))
pour h non nul
pour passer de la un à la deux, tu utilises la troisième formule, mais pas dans le même sens :
=1-2\sin^2(a))
équivaut à
=1-cos(2a))
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 17:33
par theluckyluke » 06 Déc 2006, 17:33
voilà, c'est bon?
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 17:37
par tonypeter » 06 Déc 2006, 17:37
EDIT: OK tout marche merci beaucoup! Je reviens si j'ai encore des problèmes :we:
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 18:19
par tonypeter » 06 Déc 2006, 18:19
Je reviens avec une autre question:
Déterminer les limites de

et
}{(h/2))
Quand h tend vers 0, sin(h/2) tend vers 0 donc
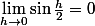
Quand h tend vers 0, sin(h/2) tend vers 0 et h/2 tend vers 0 donc
}{(h/2))
et la je bloque!!

??????????
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 18:43
par tonypeter » 06 Déc 2006, 18:43
Petit UP
C'est un DM pour demain, je n'y arrive absolument pas.......
Merci
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 06 Déc 2006, 19:06
par theluckyluke » 06 Déc 2006, 19:06
tonypeter a écrit:Je reviens avec une autre question:
Déterminer les limites de

et
}{(h/2))
Quand h tend vers 0, sin(h/2) tend vers 0 donc
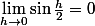
Quand h tend vers 0, sin(h/2) tend vers 0 et h/2 tend vers 0 donc
}{(h/2))
et la je bloque!!

??????????
0/0 est une forme indeterminée, il faut que tu te débrouilles pour l'enlever
a vue d'oeil, il faut peut etre utiliser la question précédente avec les égalités
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 19:10
par tonypeter » 06 Déc 2006, 19:10
EDIT: En fait j'ai oulié de lire une petite précision:
"On admet que
/x =1)
"
:mur:
Donc la limite de la 2ème expression est 1!
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 19:32
par tonypeter » 06 Déc 2006, 19:32
Encore un problème!!
Démontrer que pour tout réel a et pour tout réel h:
-\sin(a)}{h}=-\sin(a)\frac{1-\cos(h)}{h}+\cos(a)\frac{\sin(h)}<br />{h})
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 20:20
par tonypeter » 06 Déc 2006, 20:20
Petit up...
-
tonypeter
- Membre Naturel
- Messages: 38
- Enregistré le: 11 Oct 2006, 18:04
-
 par tonypeter » 06 Déc 2006, 20:40
par tonypeter » 06 Déc 2006, 20:40
Vraiment personne n'a d'idée?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
et
et la je bloque!!
??????????