Bonjour,
Je cherche à résoudre un problème de thermique décrit par l'équation différentielle suivante :
Y'(t) = A * Y(t)^4 + B oú A et B sont des constantes
Les conditions aux limites sont les suivantes:
Y(0) = Y0 ; Y'(0) = 0
J'ai essayé avec l'équation de Bernoulli mais malheureusement je n'y suis pas parvenu et je ne suis même pas certain qu'elle soit applicable lorsqu'il y a une constante isolée comme c'est le cas ici avec B.
Quelqu'un pourrait-il m'eclairer ?
Merci d'avance !
Corentin
Équation différentielle non linéaire
6 messages
- Page 1 sur 1
Re: Équation différentielle non linéaire
Ton equation est à variables séparables et se résout en intégrant 
Il suffit de décomposer en éléments simples .
en éléments simples .
Il suffit de décomposer
Re: Équation différentielle non linéaire
Bonjour Tournesol et merci pour l'aide !
J'ai suivi tes conseils, j'ai commencé par faire le changement de variable Y=y^2 pour me ramener à un polynôme de 2nd degré.
J'ai trouvé le delta (positif) puis les racines réelles x1 et x2. Ensuite j'ai factorisé le polynôme:
(Y-x2))
Puis je suis repassé sur la variable y^2 et j'ai trouvé une factorisation supplémentaire:
(y^2-x2)=A(y+\sqrt(x1))(y-\sqrt(x2))(y^2-x2))
Le polynôme (y^2-x2) a un discriminant négatif et est donc non factorisable sur R.
J'ai donc effectué la décomposition en éléments simples suivante:
)(y-\sqrt(x1))(y^2-x2)}=\frac{1}{A}*(\frac{K1}{y+\sqrt(x1)}+\frac{K2}{y-\sqrt(x1)}+\frac{K3y+K4}{y^2-x2}))
J'ai trouvé les valeurs de K1, K2, K3, K4.
Je me retrouve cependant dans une impasse, je ne sais pas vraiment comment partir pour résoudre cette équation différentielle:
}+\frac{K2}{y-\sqrt(x1)}+\frac{K3y+K4}{y^2-x2})=1)
Merci encore !
Corentin
J'ai suivi tes conseils, j'ai commencé par faire le changement de variable Y=y^2 pour me ramener à un polynôme de 2nd degré.
J'ai trouvé le delta (positif) puis les racines réelles x1 et x2. Ensuite j'ai factorisé le polynôme:
Puis je suis repassé sur la variable y^2 et j'ai trouvé une factorisation supplémentaire:
Le polynôme (y^2-x2) a un discriminant négatif et est donc non factorisable sur R.
J'ai donc effectué la décomposition en éléments simples suivante:
J'ai trouvé les valeurs de K1, K2, K3, K4.
Je me retrouve cependant dans une impasse, je ne sais pas vraiment comment partir pour résoudre cette équation différentielle:
Merci encore !
Corentin
Re: Équation différentielle non linéaire
Tu devrais nous donner tes constantes A et B afin que nous puissions vérifier .
Re: Équation différentielle non linéaire
Bonjour Tournesol !
Voici les constantes:
A = -5.9E-13
B = 1.52E-10
Je trouve x1 = -x2 = 16
Corentin
Voici les constantes:
A = -5.9E-13
B = 1.52E-10
Je trouve x1 = -x2 = 16
Corentin
Re: Équation différentielle non linéaire
Tes conditions initiales posent de sérieux pbs .
Ton équa diff est avec les CI
avec les CI =y_0) et
et =0)
En reportant dans l'équa diff , on obtient
Ton équation devient=a(y-y_0)(y+y_0)(y^2+y_0^2))
Si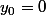 l'équation est équivalente à
l'équation est équivalente à  sur tout intervalle sur lequel y ne s'annule pas . Elle s'intègre en
sur tout intervalle sur lequel y ne s'annule pas . Elle s'intègre en 
Vrai aussi bien sur ]-1;0[ que sur ]0;1[ et on obtient une absurdité en faisant tendre x vers 0 .
La seule solution définie au voisinage de 0 est la fonction nulle .
Si , alors au voisinage de 0 y' est équivalent à
, alors au voisinage de 0 y' est équivalent à )
Cette équation s'intègre en et tes CI ne sont vérifiées que si k=0 .
et tes CI ne sont vérifiées que si k=0 .
Donc la seule solution définie au voisinage de 0 est la fonction constante égale à .
.
Cette conclusion s'applique aussi dans le cas où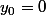
Enfin les solutions non constantes de ton équa diff vérifient
\right]=ax+k)
avec
En posant et k' une autre constante , on obtient
et k' une autre constante , on obtient
\right]+k')
Ton équa diff est
En reportant dans l'équa diff , on obtient
Ton équation devient
Si
Vrai aussi bien sur ]-1;0[ que sur ]0;1[ et on obtient une absurdité en faisant tendre x vers 0 .
La seule solution définie au voisinage de 0 est la fonction nulle .
Si
Cette équation s'intègre en
Donc la seule solution définie au voisinage de 0 est la fonction constante égale à
Cette conclusion s'applique aussi dans le cas où
Enfin les solutions non constantes de ton équa diff vérifient
avec
En posant
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
