Equation différentielle non linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Jan 2012, 20:10
par Dinozzo13 » 18 Jan 2012, 20:10
Bonjour, j'aurai besoin d'aide ou astuce pour résoudre cette équation différentielle :
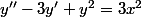
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 18 Jan 2012, 20:14
par Le_chat » 18 Jan 2012, 20:14
c'est dans quel cadre? Ca risque d'être tendu pour donner une solution explicite.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Jan 2012, 20:25
par Dinozzo13 » 18 Jan 2012, 20:25
Salut !
Comment cela dans quel cadre ?
C'est une équation que j'ai trouvée dans un livre mais qui n'est pas corrigée.
-
JackeOLanterne
- Membre Relatif
- Messages: 333
- Enregistré le: 11 Nov 2010, 00:31
-
 par JackeOLanterne » 18 Jan 2012, 22:31
par JackeOLanterne » 18 Jan 2012, 22:31
Dinozzo13 a écrit:Bonjour, j'aurai besoin d'aide ou astuce pour résoudre cette équation différentielle :
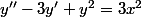
C'est une équation diff. linéaire du 2nd ordre à coeff. constants avec 2nd membre en
e^kx)
. :zen:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Jan 2012, 22:32
par barbu23 » 18 Jan 2012, 22:32
Non, regarde bien, il y'a un terme qui s'écrit :

. :zen:
-
JackeOLanterne
- Membre Relatif
- Messages: 333
- Enregistré le: 11 Nov 2010, 00:31
-
 par JackeOLanterne » 18 Jan 2012, 22:44
par JackeOLanterne » 18 Jan 2012, 22:44
barbu23 a écrit:Non, regarde bien, il y'a un terme qui s'écrit :

. :zen:
Bon, elle n'est pas linéaire (de près); ce qui n'empêche pas d'en échanger un pré-carré :
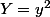
.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Jan 2012, 04:30
par Dinozzo13 » 19 Jan 2012, 04:30
Donc ? Comment résoudre cette équation différentielle ?
On effectue le changement de variable
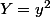
?
Mais alors on résoud
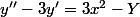
? ou on exprimer

et
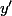
en fonction de

?
Merci d'avance :++:
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 19 Jan 2012, 17:59
par Le_chat » 19 Jan 2012, 17:59
J'ai des doutes sur le fait qu'on puisse obtenir des solutions non évidentes, il n'y aurait pas une erreur?
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 19 Jan 2012, 18:06
par el niala » 19 Jan 2012, 18:06
Le_chat a écrit:J'ai des doutes sur le fait qu'on puisse obtenir des solutions non évidentes, il n'y aurait pas une erreur?
tout à fait d'accord, j'ai aussi des doutes sur la méthode proposée par
JackOLanterne, il serait intéressant qu'il détaille :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
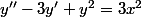
. :zen:
