Surface et volume integral

[Massi]

bonjour
Je me demande tant que le volume d'une sphère est lintegral S(x)dx alors que S(x) est la surface dun seul cercle ALORS. La question est pour quoi la lois nest pas comme ceci
V= lintegral de π*y² sans ajouter le dx , et puis cette derniere lois, resume que le volume dune sphere c'est la somme des surfaces des cercle d'un point a un autre.
Ps: je sais si on ajoute le dx sa voudrais dire que cest la somme des petit volume et c'est just . On pensant bien on peut le faire simplement on additionnant les surface des cercle

[Black Jack]

Salut,

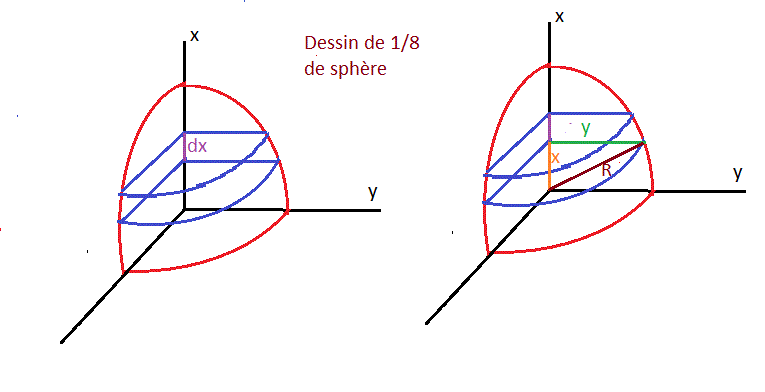
π*y² dx est le volume élémentaire d'un cylindre de rayon y et de hauteur élémentaire dx (voir dessin de gauche).

La base de ce volume élémentaire est un cercle de la sphère dans un plan parallèle à Oxy à l'ordonnée x.
On a donc x²+y² = R² (voir dessin de droite)

En faisant la somme des volumes de ces cylindres élémentaires (dont le rayon varie) pour x allant de -R à R on aura le volume de la sphère

V = Pi * S(de-RàR) y² dx
V = Pi * S(de-RàR) (R²-x²) dx
V = Pi * [R².x - x³/3](de-RàR)

V = Pi * [R²*R - R³/3 + R²*R - R³/3] = 4/3 Pi R³

[Massi]

Salut,

π*y² dx est le volume élémentaire d'un cylindre de rayon y et de hauteur élémentaire dx (voir dessin de gauche).

La base de ce volume élémentaire est un cercle de la sphère dans un plan parallèle à Oxy à l'ordonnée x.
On a donc x²+y² = R² (voir dessin de droite)

En faisant la somme des volumes de ces cylindres élémentaires (dont le rayon varie) pour x allant de -R à R on aura le volume de la sphère

V = Pi * S(de-RàR) y² dx
V = Pi * S(de-RàR) (R²-x²) dx
V = Pi * [R².x - x³/3](de-RàR)

V = Pi * [R²*R - R³/3 + R²*R - R³/3] = 4/3 Pi R³

Merci pour votre réponse. Mais la somme des surfaces des cercle egale telle au volume

[Black Jack]

Rebonjour,

Je n'ai pas fait une somme de surfaces pour trouver un volume

Ce serait une monstruosité mathématique, la relation ne serait pas homogène. (une surface n'a pas les mêmes dimensions qu'un volume)

J'ai fait une somme de VOLUMES élémentaires pour trouver le volume total.

Un volume élémentaire est ici : dV = Pi * y².dx

Pi est un nombre pur (sans dimension)
"y" étant une longueur, ---> y² a pour dimensions L² (longueur au carré)
dx est aussi une longueur (bien que "très petite"), et donc la dimension de dl est L

[Pi * y² * dx] = L² * L = L³

Donc dV = Pi * y² * dx est un VOLUME et certainement pas une surface.

Attention, ceci est beaucoup plus important que tu ne le penses probablement.

Vérifier l'homogénéité d'une relation est primordial, les 2 membres d'une équation (comme dV = Pi * y² * dx) DOIVENT avoir la même dimension (ici celle d'un volume).

dV est ici le volume élémentaire d'un cylindre dont la base a une aire de Pi.y² et de hauteur dx

[Massi]

Rebonjour,

Je n'ai pas fait une somme de surfaces pour trouver un volume

Ce serait une monstruosité mathématique, la relation ne serait pas homogène. (une surface n'a pas les mêmes dimensions qu'un volume)

J'ai fait une somme de VOLUMES élémentaires pour trouver le volume total.

Un volume élémentaire est ici : dV = Pi * y².dx

Pi est un nombre pur (sans dimension)
"y" étant une longueur, ---> y² a pour dimensions L² (longueur au carré)
dx est aussi une longueur (bien que "très petite"), et donc la dimension de dl est L

[Pi * y² * dx] = L² * L = L³

Donc dV = Pi * y² * dx est un VOLUME et certainement pas une surface.

Attention, ceci est beaucoup plus important que tu ne le penses probablement.

Vérifier l'homogénéité d'une relation est primordial, les 2 membres d'une équation (comme dV = Pi * y² * dx) DOIVENT avoir la même dimension (ici celle d'un volume).

dV est ici le volume élémentaire d'un cylindre dont la base a une aire de Pi.y² et de hauteur dx

Re rebonjour, merci beaucoup pour ton aide ,
Je sais bien quelle est non homogène alors fausse et je sais que ta fait des somme elementaire du volume. Merci jai bien comprais MAIS:
On pensant seul , je crois que faire (lintegral) ou la somme des airs avec loutil de lintegral sa va maider comme une autre solution pour calculer le volume . Une explication profonde svp sur se point que je ne comprend pas

[Black Jack]

On ne peut pas utiliser quelque chose de faux ... dans le but d'arriver plus facilement à une solution, c'est un leurre.

Il y a plusieurs manières de démontrer l'expression du volume de la sphère.

Outre celle que j'ai utilisée dans ma réponse précédente, on peut aussi :

a) Par un des théorèmes de Guldin, qui est :

Théorème — La mesure du volume engendré par la révolution d'un élément de surface plane autour d'un axe situé dans son plan et ne le coupant pas est égale au produit de l'aire de la surface par la longueur de la circonférence décrite par son centre d'inertie.

On peut donc faire tourner un demi disque autour du diamètre qui le borne

Le demi disque a pour aire : (1/2)*Pi*R² (qu'on connait par coeur ou qu'on démontre par une intégrale)

Et il faut encore calculer la distance entre le centre d'inertie du demi disque et le diamètre le bornant... cela se fait aussi via une intégrale. On trouve cette distance OG = 4R/(3.Pi)
La distance parcourue par G quand le demi disque fait un tour complet autour du diamètre bornant le demi disque est donc 2Pi * 4R/(3.Pi) = (8/3) R

Et donc le volume de la sphère est V = (1/2)*Pi*R² * (8/3)*R = (4/3).Pi.R³

b) via une intégrale triple. (en coordonnées cartésiennes)

c) via une intégrale triple. (en coordonnées sphériques)

d) via une intégrale triple. (en coordonnées cylindriques)

On trouvera toutes ces méthodes sur le net ...