Loi Exponentielle

[Tequinox]

Bonjour,
Je fais des exercices d'entrainement sur la loi Exponentielle, mais je n'arrive pas à faire le suivant :

Pour se rendre d’un endroit A à un endroit B, on peut prendre le bus ou le métro.

Le temps de trajet en métro suit une loi exponentielle de moyenne 20 minutes,
et le temps de trajet en bus est une variable indépendante de la première, de loi exponentielle de moyenne 35 minutes.

Quelle est la probabilité que le trajet en bus soit plus rapide que le trajet en métro ?

J'ai donc calculé les λ :
λa=1/20.
λb=1/35.

Mais je ne vois pas du tout ce que je suis sensé faire pour les comparer.

Pouvez-vous m'aidez, merci.

[GaBuZoMeu]

Tu as deux variables aléatoires : et , dont tu connais les densités et qui sont indépendantes, bref tu connais leur densité jointe.
On te demande la probabilité de l'événement . Une petite intégrale à calculer ...

[Tequinox]

Je n'y arrive pas, car il reste toujours des inconnus aux équations, je ne sais pas comment faire.

[GaBuZoMeu]

Taratata, tout se calcule parfaitement. D'ailleurs, de quelles équations parles-tu ? Explique un peu ce que tu fais.
Quelle est la densité jointe du couple (c'est comme il se doit une fonction de deux variables réelles) ?

[Tequinox]

Je ne sais pas si je calcul correctement la densité jointe :

Comme ce sont des variables indépendantes je fais :

d(Tm,Tb)= (λa*e^(λa*m) )*(λb*e^(λb*b))
d(Tm,Tb)= (0.05*e^(0.05*m) )*(1/35*e^(1/35*b))

Mais je ne sais pas par quoi remplacer m et b.

[GaBuZoMeu]

Par rien, ce sont des variables : une variable m pour le temps de parcours en métro et une variable b pour le temps de parcours en bus.
Une petite remarque : la densité jointe que tu donnes n'est valable que pour m et b vérifiant des inégalités : tu vois lesquelles ?
Les deux variables sont les coordonnées d'un point du plan. L'événement "le temps de parcours en bus est inférieur ou égal au temps de parcours en métro" correspond à un domaine dans ce plan, et la probabilité de l'événement est l'intégrale de la densité jointe sur ce domaine.

[Tequinox]

C'est valable que si d(Tm,Tb)= (0.05*e^(0.05*m) )*(1/35*e^(1/35*b)) = 1 ?

Je sais que p(X>t)=e^(-λt)

Et je pense que pour résoudre l'exercice, il faut faire p (Tb>Tm) mais je ne vois pas comment appliquer la propriété ci dessus.

[GaBuZoMeu]

Tu es perdu et tu écris un peu n'importe quoi.
Tu as deux variables aléatoires réelles positives.
L'ensemble des valeurs prises par ce couple de variables aléatoires est le quadrant positif .
Tu as un événement qui est une partie de ce quadrant, et tu connais la densité jointe. Tu obtiens la probabilité de l'événement en intégrant la densité jointe sur la partie du quadrant correspondant à l'événement. C'est à ça que sert la densité non ?

[Tequinox]

C'est le premier exercice qui demande des calculs de densité jointe, je n'en n'avais encore jamais vu.
J'ai beau chercher, je ne comprend ce qu'il faut faire, c'est pas grave, dommage.

[GaBuZoMeu]

J'avais l'impression que tu connaissais la notion de densité jointe, ce n'est pas le cas ? Tu dis ne pas savoir quoi faire, il me semble pourtant avoir été assez explicite.

Le domaine du plan correspondant à l'événement "le trajet en bus dure moins que celui en métro" est tout simplement le domaine défini par . Intégrer sur ce domaine la densité jointe que tu as toi-même donnée :



ce n'est pas la mer à boire, si ?

[LB2]

Hello,

si tu n'as pas vu les intégrales doubles et les densités jointes, il est possible d'obtenir le résultat en appliquant la formule des probabilités totales pour calculer la fonction de répartition de la variable aléatoire Tb-Tm par une intégrale simple, puis de regarder la valeur de cette fonction de répartition en 0.

[GaBuZoMeu]

Le résultat 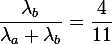est intuitivement assez clair. Je me demande si on peut y arriver plus directement que par les calculs un peu bourrins proposés jusqu'ici.

[tournesol]

LB2 , j'attend ta solution avec impatience . Je ne sais pas faire cela .
Bon il faudrait que je révise . Je sais ...

[tournesol]

OK LB2 .J'ai trouvé . Je n'avais pas compris que "utiliser la formule des probabilités totales" veut dire en continu "utiliser l'espérance conditionnelle " .
Ce que j'en pense , c'est que lorsqu'on etudie l'espérance conditionnelle , on a fait de la théorie de la mesure et donc déjà étudié les intégrales multiples .

[LB2]

Je pensais à la méthode décrite par Alex P. Miller dans ce fil : https://math.stackexchange.com/q/1523349

[tournesol]

Merci pour ton indication . C'est exactement ce que j'avais fait pour trouver mais sans trop de convictions . J'ai besoin de réviser tout cela .

[GaBuZoMeu]

Personne n'a donc d'idée pour voir directement le résultat ? Pourtant, dans la première réponse (la plus cotée) du fil de StackExchange, le est asséné comme allant de soi.

[tournesol]

la réponse est : moyenne métro / ( moyenne métro + moyenne bus )
Ce résultat se généralise-t-il ?
On peut essayer avec les densités et qui donnent b et m pour moyennes respectives . Ou avec des densités plus simples à intégrer .

[tournesol]

la réponse est : moyenne métro / ( moyenne métro + moyenne bus )
Ce résultat se généralise-t-il ?
On peut essayer avec les densités et qui donnent b et m pour moyennes respectives . Ou avec des densités plus simples à intégrer .

[GaBuZoMeu]

Ce n'est bien sûr pas le cas en général (penser au cas dégénéré où les variables aléatoires sont en fait constantes !).
L'argument heuristique que je vois : les probabilités de terminer dans un petit temps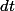 sont et . La probabilité que si l'un des deux termine dans le temps 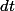, ce soit celui de paramètre est . Et ceci est valable à n'importe quel temps positif. Pas de calcul, certes, mais assez olé-olé.